


Next: u_eigen
Up: u_eigen
Previous: u_eigen
7. A survey of
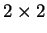 cases
cases
So far we have not discussed whether all
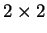 matrices are
like the three examples--and they aren't! On the other hand, not
many different kinds of things can happen. Here are the
typical cases:
matrices are
like the three examples--and they aren't! On the other hand, not
many different kinds of things can happen. Here are the
typical cases:
- Diagonal matrices. There are two subcases:
- Scalar matrices
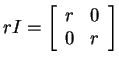 . Here
the only eigenvalue is
. Here
the only eigenvalue is
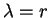 and every nonzero vector is
an eigenvector.
and every nonzero vector is
an eigenvector.
- Diagonal matrices with distinct diagonal entries
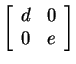 with
with 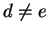 . Here
the eigenvectors lie on the
. Here
the eigenvectors lie on the 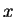 - and
- and 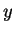 -axes and the
eigenvalues are just the diagonal entries.
-axes and the
eigenvalues are just the diagonal entries.
- Symmetric matrices, other than scalar matrices. In
this case, there are two real eigenvalues and the eigenspaces (eigenvector
directions) are orthogonal. See for instance the example in Figure
![[*]](/lib/latex2html-icons/crossref.gif) .
.
- Matrices with two distinct real eigenvalues, as in the example
in Figure
![[*]](/lib/latex2html-icons/crossref.gif) . Here there are two eigenspaces (lines of eigenvectors).
. Here there are two eigenspaces (lines of eigenvectors).
- Matrices with no real eigenvalues, such as a
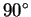 rotation. In this case there are no
real eigenvectors either. However, if we are willing to use
complex numbers then these matrices are like the previous case;
they do have complex eigenvalues with corresponding eigenvectors.
rotation. In this case there are no
real eigenvectors either. However, if we are willing to use
complex numbers then these matrices are like the previous case;
they do have complex eigenvalues with corresponding eigenvectors.
- Matrices that have only one eigenvalue,
other than scalar matrices. Examples are (i)
shears, such as the matrix
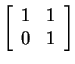 ; (ii) nonzero
matrices that are ``nilpotent'', which means some power is the
zero matrix, for example
; (ii) nonzero
matrices that are ``nilpotent'', which means some power is the
zero matrix, for example
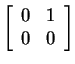 ; and (iii)
nilpotent matrices added to scalar matrices, as in
; and (iii)
nilpotent matrices added to scalar matrices, as in
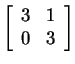 . These are strange in many ways. For
example, they have only one line of eigenvectors.
. These are strange in many ways. For
example, they have only one line of eigenvectors.
Non-scalar
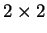 matrices with only one eigenvalue are
called ``defective''.
matrices with only one eigenvalue are
called ``defective''.
You can begin to see how any
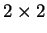 matrix must be like one
of these examples:
matrix must be like one
of these examples:
- Find the characteristic polynomial, which has degree 2.
- Factor it to get the roots (eigenvalues). You may need to
use the quadratic formula, and the roots might be complex.
- If the roots are real and distinct (different),
then we get the two lines of eigenvectors in
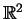 .
.
- If the roots are are identical (for example, if the
characteristic polynomial is
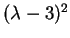 ), then the
matrix is either scalar or else is case
), then the
matrix is either scalar or else is case ![[*]](/lib/latex2html-icons/crossref.gif) .
.
- Finally, if the roots are complex rather than real (in which
case they are distinct), the matrix fits case
![[*]](/lib/latex2html-icons/crossref.gif) .
.
All this is assuming that the matrix has real entries, but these
cases are pretty much the same even for matrices with complex
entries.
It turns out that even
 matrices split into pieces that
fit these cases.
matrices split into pieces that
fit these cases.
Problem
U-10. Classify the eight examples in the handout with pictures
of a house according to this scheme. (The first example is the
identity matrix.)
Problem
U-11. Show that a
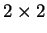 matrix is diagonalizable if and
only if it is not defective. [This problem really should go after
the next section. Also, ``diagonalizable'' here means possibly
using complex numbers.]
matrix is diagonalizable if and
only if it is not defective. [This problem really should go after
the next section. Also, ``diagonalizable'' here means possibly
using complex numbers.]



Next: u_eigen
Up: u_eigen
Previous: u_eigen
Kirby A. Baker
2001-11-20
![]() matrices are
like the three examples--and they aren't! On the other hand, not
many different kinds of things can happen. Here are the
typical cases:
matrices are
like the three examples--and they aren't! On the other hand, not
many different kinds of things can happen. Here are the
typical cases:
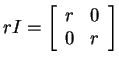 . Here
the only eigenvalue is
. Here
the only eigenvalue is
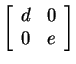 with
with 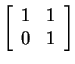 ; (ii) nonzero
matrices that are ``nilpotent'', which means some power is the
zero matrix, for example
; (ii) nonzero
matrices that are ``nilpotent'', which means some power is the
zero matrix, for example
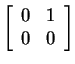 ; and (iii)
nilpotent matrices added to scalar matrices, as in
; and (iii)
nilpotent matrices added to scalar matrices, as in
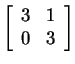 . These are strange in many ways. For
example, they have only one line of eigenvectors.
. These are strange in many ways. For
example, they have only one line of eigenvectors.
![]() matrices with only one eigenvalue are
called ``defective''.
matrices with only one eigenvalue are
called ``defective''.
![]() matrix must be like one
of these examples:
matrix must be like one
of these examples:
![]() matrices split into pieces that
fit these cases.
matrices split into pieces that
fit these cases.
![]() matrix is diagonalizable if and
only if it is not defective. [This problem really should go after
the next section. Also, ``diagonalizable'' here means possibly
using complex numbers.]
matrix is diagonalizable if and
only if it is not defective. [This problem really should go after
the next section. Also, ``diagonalizable'' here means possibly
using complex numbers.]