6. Easy facts

Notice that the characteristic polynomial is easy to find if the matrix $A$ is diagonal or even triangular:

Observation 1. The eigenvalues of a triangular matrix are just the diagonal entries.

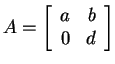Why? For the case of an upper-triangular $2 \times 2$ matrix, $A = \matp{rr}{a&b\\ 0&d}$, notice that 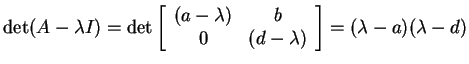$\det (A - \lambda I) = \det \matp{cc}{(a-\lambda)&b\\ 0&(d-\lambda)}= (\lambda-a)(\lambda-d)$, so the roots are $a$ and $d$. Larger matrices and lower-triangular matrices work the same.

Another easy fact:

Observation 2. $A$ and $A ^ t$ have the same characteristic polynomial.

The reason is that a matrix and its transpose have the same determinant, so $\det (A-\lambda I) ^ t = \det (A-\lambda I)$, or equivalently, $\det( A - \lambda I ^ t) = \det (A - \lambda I)$, or equivalently, $p _ {A ^ t}(\lambda ) = p _ A(\lambda)$.

Problem U-8. A stochastic matrix is a square matrix such as 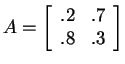$A = \matp{rr}{.2&.7\\ .8&.3}$ in which the entries are $\geq 0$ and each column has sum 1. Stochastic matrices have many applications, for example to shifts in populations over time. Let's stick to the $2 \times 2$ case for convenience, but larger cases work the same.

(a) Show that a $2 \times 2$ matrix has row sums all equal to 1 if and only if $\matp{c}{1\\ 1}$ is an eigenvector for the eigenvalue 1.

(b) Use Observation 2 to show that a stochastic $2 \times 2$ matrix has the eigenvalue 1. This is the same thing as having a nonzero vector v with $T($v$) =$   v, or in other words, a nonzero ``fixed vector''.

(c) Find a nonzero fixed vector for $A$.

Problem U-9. Explain: If $A$ has the eigenvalue 0, then the eigenvectors for the eigenvalue 0 are all in the kernel of $A$, and $A$ is singular.