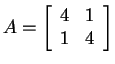 . But
instead of showing the usual unit square and its image (a parallelogram),
the figure shows a special slanted square and its image. Also shown are the
vectors
v
. But
instead of showing the usual unit square and its image (a parallelogram),
the figure shows a special slanted square and its image. Also shown are the
vectors
vMany linear transformations are like diagonal transformations if you look at them the right way--they are ``diagonalizable''. If the matrix is not already diagonal, we need to choose a new basis, representing new axes.
Figure ![]() shows the effects of the
transformation
shows the effects of the
transformation ![]() for
for
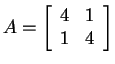 . But
instead of showing the usual unit square and its image (a parallelogram),
the figure shows a special slanted square and its image. Also shown are the
vectors
v
. But
instead of showing the usual unit square and its image (a parallelogram),
the figure shows a special slanted square and its image. Also shown are the
vectors
v![]() ,
v
,
v![]() along the square, and their images.
along the square, and their images.
Problem
U-2. Find
![]() v
v![]() and
and
![]() v
v![]() numerically
and see how they relate to
v
numerically
and see how they relate to
v![]() and
v
and
v![]() . Here
v
. Here
v and
v
and
v .
.
Problem
U-3. Show that the matrix of ![]() relative to the new
basis
v
relative to the new
basis
v![]() ,
v
,
v![]() is a diagonal matrix,
specifically, the diagonal matrix
is a diagonal matrix,
specifically, the diagonal matrix
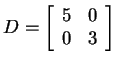 .
.