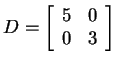 . Here
are some ways in which
. Here
are some ways in which
As you have seen in the past, diagonal matrices are especially
easy. They represent problems in which the variables work
separately. For example, let
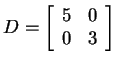 . Here
are some ways in which
. Here
are some ways in which ![]() is easy:
is easy:
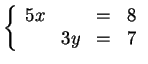 ,
easily solved separately.
,
easily solved separately.
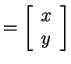 , we have
, we have
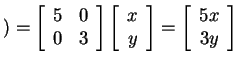 , a nonuniform
scaling in which
, a nonuniform
scaling in which
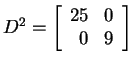 , obtained by treating each
diagonal entry separately.
, obtained by treating each
diagonal entry separately.
Figure ![]() shows what
shows what ![]() does to a unit square and vectors
along the
does to a unit square and vectors
along the ![]() - and
- and ![]() -axes.
-axes.
Problem
U-1. What, specifically, does ![]() do to vectors along the
do to vectors along the ![]() -axis?
Along the
-axis?
Along the ![]() -axis? How about a vector pointing left along the
-axis? How about a vector pointing left along the ![]() -axis?
-axis?