


Next: u_eigen
Up: u_eigen
Previous: u_eigen
2. How to locate the new axes
The key to finding the new basis is to compare what happens to
vectors on and off the desired axes. In Figures ![[*]](/lib/latex2html-icons/crossref.gif) and
and
![[*]](/lib/latex2html-icons/crossref.gif) , what do you notice?
, what do you notice?
Figure:
A diagonal transformation again
|
udir/diag2.eps |
Figure:
A diagonalizable transformation
|
udir/secret2.eps |
Notice that a vector on either of the desired axes has an
image along the same line. In other words, it has been
multiplied by a scalar. In contrast, for a vector not on one
of the desired axes, its image is not along the same line.
This is the key! For any matrix transformation 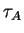 , we
look for vectors that get multiplied by a scalar. These tell us
the new axes to use. As you will see, they are easy to compute.
, we
look for vectors that get multiplied by a scalar. These tell us
the new axes to use. As you will see, they are easy to compute.
Definition. A nonzero vector
v with
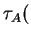 v
v v for some scalar
v for some scalar 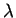 is called an
eigenvector of
is called an
eigenvector of 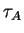 . The scalar
. The scalar 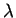 is the
corresponding eigenvalue1.
is the
corresponding eigenvalue1.
Notes.
- It is traditional to use the Greek letter
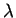 (lambda) for the scalar. This seems strange at first, but it's really
helpful, in that when you see statements with
(lambda) for the scalar. This seems strange at first, but it's really
helpful, in that when you see statements with 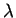 you
immediately realize they are about eigenvalues.
you
immediately realize they are about eigenvalues.
- Figures
![[*]](/lib/latex2html-icons/crossref.gif) and
and ![[*]](/lib/latex2html-icons/crossref.gif) show
show 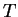 applied to
just one vector not on the axes, but other vectors would behave similarly.
applied to
just one vector not on the axes, but other vectors would behave similarly.
- All we need is to choose one vector on each new axis for a new
basis. Any nonzero vector along the axis will do.
- The new axes are lines through the origin and so are subspaces. Therefore
they are called eigenspaces for
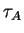 . We'll emphasize eigenvectors
for the present, but it's actually the eigenspaces that are the neater concept.
. We'll emphasize eigenvectors
for the present, but it's actually the eigenspaces that are the neater concept.
- In general, for a
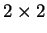 matrix
matrix 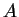 , there can be either
two, one, or no eigenspaces. If there are two, then you can make a new
basis from two eigenvectors and get a diagonal matrix relative to the
new basis. In this case,
, there can be either
two, one, or no eigenspaces. If there are two, then you can make a new
basis from two eigenvectors and get a diagonal matrix relative to the
new basis. In this case, 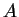 is said to be diagonalizable.
is said to be diagonalizable.
- In the more general setting
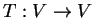 , where
, where 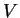 is a
vector space, the concept is the same: If
is a
vector space, the concept is the same: If
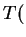 v
v v for a
nonzero vector
v, then
v is an eigenvector and
v for a
nonzero vector
v, then
v is an eigenvector and 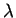 is
an eigenvalue.
is
an eigenvalue.
- For a matrix transformation
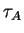 , to say ``
v is
an eigenvector of
, to say ``
v is
an eigenvector of 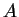 '' is the same thing as saying ``
v is
an eigenvector of
'' is the same thing as saying ``
v is
an eigenvector of 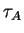 .'' Obviously,
v is an
eigenvector of
.'' Obviously,
v is an
eigenvector of 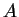 when
v is nonzero and
when
v is nonzero and
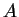 v
v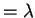 v for some scalar
v for some scalar 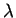 .
.
- An eigenvalue could be negative, so that
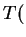 v
v points in the
opposite direction from
v. An eigenvalue can even be 0. (An
eigenvector must be nonzero, though.)
points in the
opposite direction from
v. An eigenvalue can even be 0. (An
eigenvector must be nonzero, though.)
- There is still the question of how to compute
eigenvectors and eigenvalues, even for
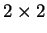 matrices; this
question will be answered below.
matrices; this
question will be answered below.



Next: u_eigen
Up: u_eigen
Previous: u_eigen
Kirby A. Baker
2001-11-20
![]() and
and
![]() , what do you notice?
, what do you notice?
![]() , we
look for vectors that get multiplied by a scalar. These tell us
the new axes to use. As you will see, they are easy to compute.
, we
look for vectors that get multiplied by a scalar. These tell us
the new axes to use. As you will see, they are easy to compute.
![]() v
v![]() v for some scalar
v for some scalar ![]() is called an
eigenvector of
is called an
eigenvector of ![]() . The scalar
. The scalar ![]() is the
corresponding eigenvalue1.
is the
corresponding eigenvalue1.