3. Another example

The example in Figure is especially neat, because the new axes are orthogonal (perpendicular to each other). This is not the situation in general. For the matrix $A = \matp{rr}{7&-4\\ 2&1}$, we do get two new axes (eigenspaces), but they are not orthogonal, as seen in Figure :

Figure: Eigenvectors in another example

udir/another.eps

Problem U-4. Check that v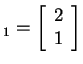$_ 1 = \matp{r}{2\\ 1}$ and v$_ 1 = \matp{r}{1\\ 1}$ are both eigenvectors of $\tau _ A$ for $A = \matp{rr}{7&-4\\ 2&1}$. What are the corresponding eigenvalues?

Problem U-5. Verify algebraically that v$=$   v$_ 1 +$   v$_ 2$ is not an eigenvector of $A$. (Check that $\tau _ A ($v$)$ is not a scalar times v.)

Problem U-6. Explain why a rotation of $\mathbb{R}^ 2$ by $90 ^ \circ$ can't have any eigenvectors. (Interestingly, if we use complex numbers, though, it does.)