As a warmup, first recall that a square matrix ![]() is ``singular'' if
many equivalent conditions occur:
is ``singular'' if
many equivalent conditions occur:
![]() ,
, ![]() has no inverse,
has no inverse,
![]() is
is
![]() but has rank less than
but has rank less than ![]() , the nullspace of
, the nullspace of
![]() has dimension
has dimension ![]() (so
(so
![]() v
v![]() 0 has a nonzero solution
v),
and so on. We'll need the first and last of these conditions. In other
words, remember that
0 has a nonzero solution
v),
and so on. We'll need the first and last of these conditions. In other
words, remember that
![]() v
v![]() 0 has a nonzero solution
v if and
only if
0 has a nonzero solution
v if and
only if
![]() .
.
Here is how to invent the method:
Given ![]() , start with the equation
, start with the equation
![]() v
v![]() v. At this
point, we don't yet know what the possible values of
v. At this
point, we don't yet know what the possible values of ![]() might be, or what nonzero vector
v might go with
might be, or what nonzero vector
v might go with ![]() .
.
As in ordinary algebra, put everything on one side:
![]() v
v![]() v
v![]() 0.
0.
Also as in ordinary algebra, it is tempting to try to factor out
v,
but this doesn't work because
![]() doesn't make sense. You
can't have a scalar minus a matrix!
doesn't make sense. You
can't have a scalar minus a matrix!
A trick to get around this is to replace
![]() v by
v by
![]() v,
where
v,
where ![]() is an identity matrix. If
is an identity matrix. If ![]() is
is
![]() ,
for example, then
,
for example, then
 . So we can write
. So we can write
![]() v
v![]() v
v![]() 0 and then get
0 and then get
![]() v
v![]() 0.
0.
Example: For
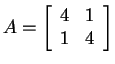 ,
,
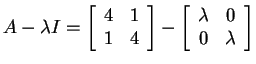
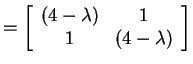 .
.
Next, from the warmup we notice that
![]() v
v![]() 0 is possible
for a nonzero vector
v if and only if
0 is possible
for a nonzero vector
v if and only if
![]() .
In the example, we see that
.
In the example, we see that
![]() . We need
to set this expression equal to 0 and solve.
. We need
to set this expression equal to 0 and solve.
In other words, the values of ![]() we are looking for are the
roots of the polynomial
we are looking for are the
roots of the polynomial
![]() . This polynomial is
called the characteristic polynomial of
. This polynomial is
called the characteristic polynomial of ![]() , denoted here
by
, denoted here
by
![]() .
.
Find the roots using algebra:
![]() factors to
factors to
![]() , so
, so
![]() or
or
![]() . Therefore the eigenvalues of
. Therefore the eigenvalues of ![]() are 5 and 3
(in this example).
are 5 and 3
(in this example).
To find eigenvectors, consider each eigenvalue separately. For the
eigenvalue 5, for example, we need to find a nonzero vector
v
with
![]() v
v![]() v, or equivalently,
v, or equivalently,
![]() v
v![]() 0. This is just
a set of linear equations!
0. This is just
a set of linear equations!
In the example, for
![]() we have
we have
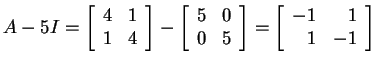 , so if we write
v
, so if we write
v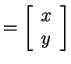 ,
,
![]() v
v![]() 0 becomes
0 becomes
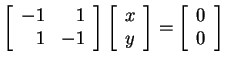 , or equivalently,
, or equivalently,
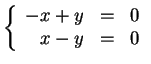 .
.
This set of equations is singular, with both equations giving
the same information. Singular systems of equations may have
seemed bad in the past, but here they are good, because we do
want a nonzero solution. Also, it's no surprise, because we
purposely chose ![]() so
so
![]() is singular.
is singular.
Choose any nonzero solution, say ![]() ,
, ![]() . In other words,
we have found that
. In other words,
we have found that
 is an eigenvector.
is an eigenvector.
Similarly, for the eigenvalue ![]() , we get
, we get
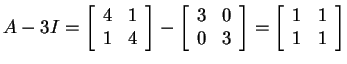 , so
, so
![]() v
v![]() 0 becomes
0 becomes
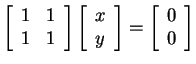 , or equivalently,
, or equivalently,
 . Let's choose the nonzero
solution
. Let's choose the nonzero
solution ![]() ,
, ![]() . We have found that
. We have found that
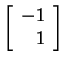 is
an eigenvector. (
is
an eigenvector. (
 would also do.)
would also do.)
To summarize the method, for given ![]() :
:
Step 1. Find the characteristic polynomial of ![]() by expanding
by expanding
![]() . (In the next section there is a shortcut for this
when
. (In the next section there is a shortcut for this
when ![]() is
is
![]() .)
.)
Step 2. Set the characteristic polynomial ![]() and find
solutions (the roots of the characteristic polynomial). These
are the eigenvalues of
and find
solutions (the roots of the characteristic polynomial). These
are the eigenvalues of ![]() .
.
Step 3. For each eigenvalue ![]() , treat
, treat
![]() v
v![]() 0
as a set of linear equations and find a nonzero solution, which is
a corresponding eigenvector.
0
as a set of linear equations and find a nonzero solution, which is
a corresponding eigenvector.