For a square matrix ![]() , to diagonalize
, to diagonalize ![]() means to find
a square matrix
means to find
a square matrix ![]() and diagonal matrix
and diagonal matrix ![]() with
with
![]() .
.
In this case we say that ![]() diagonalizes
diagonalizes ![]() . Notice that
. Notice that
![]() has to be nonsingular or it won't have an inverse.
has to be nonsingular or it won't have an inverse.
Some matrices are ``diagonalizable'' and others are not.
![]() For
For
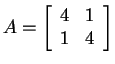 , it turns out that
, it turns out that
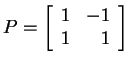 is a good matrix to diagonalize
is a good matrix to diagonalize ![]() .
In fact,
.
In fact,
![]() for
for
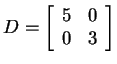 .
.
Notice that
 and
and
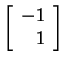 are eigenvectors
of
are eigenvectors
of ![]() . In fact,
. In fact, ![]() is always made from eigenvectors:
is always made from eigenvectors:
Proposition. For
![]() matrices
matrices ![]() and
and ![]() ,
,
![]() diagonalizes
diagonalizes ![]()
![]() the columns of
the columns of ![]() are
linearly independent eigenvectors of
are
linearly independent eigenvectors of ![]() and the diagonal
entries of
and the diagonal
entries of ![]() are the corresponding eigenvalues.
are the corresponding eigenvalues.
(The linear independence of columns is needed in order for ![]() to be nonsingular. It wouldn't work, for instance, to have all
columns be the same. For the reasoning behind the Proposition,
see below.)
to be nonsingular. It wouldn't work, for instance, to have all
columns be the same. For the reasoning behind the Proposition,
see below.)
The Proposition tells how to diagonalize ![]() : Just find the
eigenvalues and corresponding eigenvectors. If there are enough
linearly independent eigenvectors, use them for the columns
of
: Just find the
eigenvalues and corresponding eigenvectors. If there are enough
linearly independent eigenvectors, use them for the columns
of ![]() . The Example could be found that way.
. The Example could be found that way.
Handy facts:
(1) Eigenvectors that belong to distinct eigenvalues are linearly
independent. Therefore, if ![]() is
is
![]() and has
and has ![]() distinct eigenvalues, then
distinct eigenvalues, then ![]() is diagonalizable. (``Distinct''
means ``all different from one another''.)
is diagonalizable. (``Distinct''
means ``all different from one another''.)
(2) A real symmetric matrix can always be diagonalized, even
if the eigenvalues are not all distinct (for example, if the
characteristic polynomial factors as
![]() ), we would say the eigenvalues are
), we would say the eigenvalues are ![]() , not
all distinct.
, not
all distinct.
These two facts will be proved in class. Let's go back and prove the Proposition.
Proof of the Proposition. For ``
![]() '': To says that
'': To says that
![]() diagonalizes
diagonalizes ![]() means that
means that
![]() . If
we take this equation and multiply both sides by
. If
we take this equation and multiply both sides by ![]() on the
left, we get
on the
left, we get ![]() . Now let's try to interpret this second
equation using eigenvalues and eigenvectors. We need two facts:
. Now let's try to interpret this second
equation using eigenvalues and eigenvectors. We need two facts:
For example,
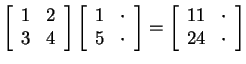 and it doesn't matter what the
other entries are.
and it doesn't matter what the
other entries are.
For example,
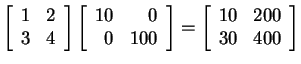 .
.
We still need to prove ``
![]() '' in the Proposition. We start
by assuming we are given
'' in the Proposition. We start
by assuming we are given ![]() and
and ![]() such that the columns of
such that the columns of
![]() are eigenvectors of
are eigenvectors of ![]() and are linearly independent.
The same two facts as before show that
and are linearly independent.
The same two facts as before show that ![]() . Since the columns
of
. Since the columns
of ![]() are linearly independent,
are linearly independent, ![]() has rank
has rank ![]() and is
invertible. Multiply both sides of
and is
invertible. Multiply both sides of ![]() on the left by
on the left by ![]() ;
we get
;
we get
![]() , as required.
, as required.
Problem
U-12. Diagonalize
 . (Use Problem U-
. (Use Problem U-![]() .)
.)
Problem
U-13. Explain how to interpret the equation
![]() in
terms of a change of basis. What is the transformation? The old basis?
The matrix relative to the old basis? The new basis? The transition matrix?
The matrix relative to the new basis?
in
terms of a change of basis. What is the transformation? The old basis?
The matrix relative to the old basis? The new basis? The transition matrix?
The matrix relative to the new basis?