Definition. For a square matrix ![]() and scalar
and scalar ![]() ,
the eigenspace of
,
the eigenspace of ![]() consists of all
v with
consists of all
v with
![]() v
v![]() v. We can call the eigenspace
v. We can call the eigenspace
![]() . In other
words,
. In other
words,
![]() consists of all eigenvectors for
consists of all eigenvectors for ![]() and also the zero vector.
and also the zero vector.
One advantage of talking about eigenspaces instead of eigenvectors is
that it's OK to talk about
![]() even when
even when ![]() is
not an eigenvalue of
is
not an eigenvalue of ![]() ; in that case,
; in that case,
![]() 0
0![]() .
.
Another advantage is that it's easier to think about examples such as ![]() ,
where
,
where ![]() is the whole space, or
is the whole space, or
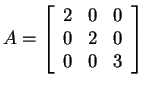 ,
where
,
where ![]() is a plane.
is a plane.
Problem
U-14. Explain:
![]() is the nullspace of
is the nullspace of
![]() ,
or equivalently, the kernel of
,
or equivalently, the kernel of
![]() . Therefore
. Therefore
![]() is always a subspace.
is always a subspace.
Problem
U-15. In each case, make up an example of a
![]() matrix
so that
matrix
so that ![]() is (a)
is (a)
![]() 0
0![]() , (b) a line, (c) a plane,
(d) all of
, (b) a line, (c) a plane,
(d) all of
![]() . (Suggestion: Use diagonal matrices.)
. (Suggestion: Use diagonal matrices.)