General interests currently include kinetic theory for evolving populations, first passage times, stochastic processes applied to biophysics, adaptive immunology models, and psychophysics models
OLD RESEARCH:
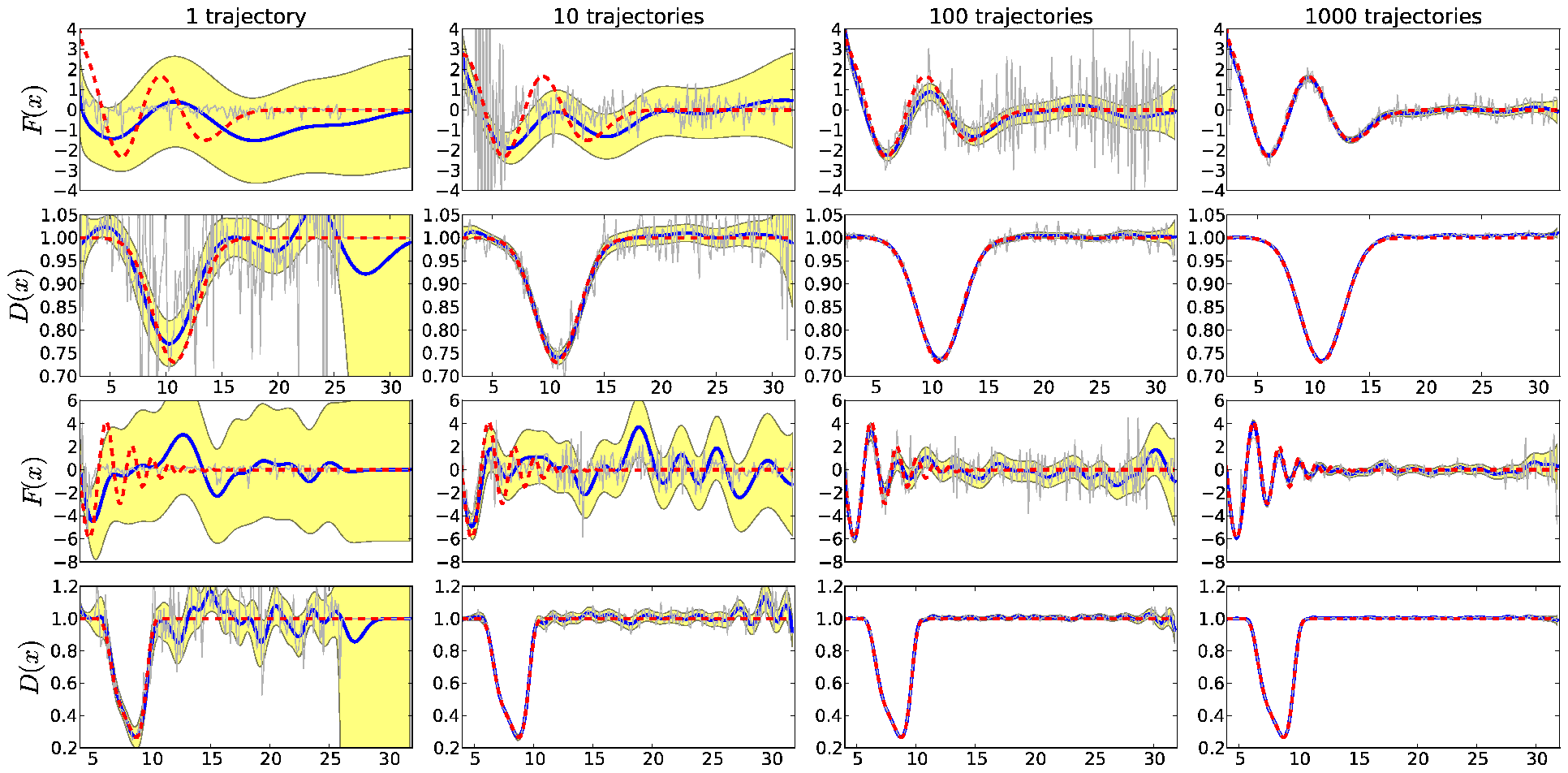
Inverse problems in PDEs and stochastic processes A major research thrust in my group is the study of inverse problem, particularly in estimating parameter functions in PDEs and SDEs. Problems of biological and biophysical importance include reconstruction of macromolecular energy profiles from single-molecule force spectroscopy experiments, estimating branching time distributions in dividing cells, and source and coefficient recovery from data described by classical PDEs. Optimization approaches and Bayesian regularization approaches, cast in the form of path integrals, have been used to reconstruct complex bond potentials from simulated data. We plan to further exploit these methods as well as L1 optimization in order to "source recover" forces exerted by cells and tissues.
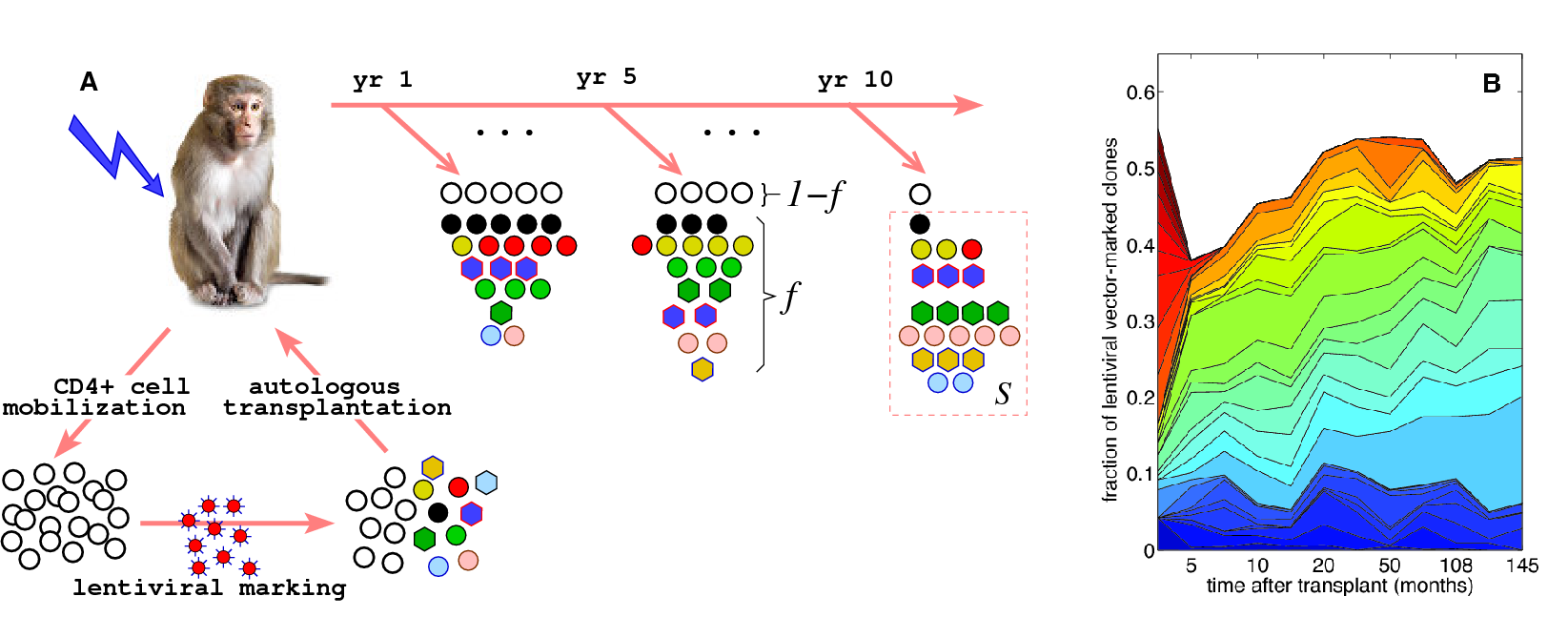
Modeling hematopoeisis and stem cell transplantation In collaboration with Prof. Irvin Chen, we are developing kinetic and statistical models to guide understanding of clonal repopulation in hematopoiesis. Autologous transplantation of lentivirus-tagged stem cells in rhesus macaque result in distinctive clone size distributions of differentiated blood. We have shown this distribution, when properly rescaled, is stationary after a few montsh post-transplant. Models of stem cell differentiation with regulation will be motivated and fit to data. Preliminary results indicate that good fits of data to simple models can be achieved with just two physiological parameters. We are also modeling thymic function after bone marrow transplant based on data from BLT mice. Our models and data analysis will be used to estimate total T cell number and diversity, potentially providing guidance for optimizing bone marrow transplant and gene therapy protocols.
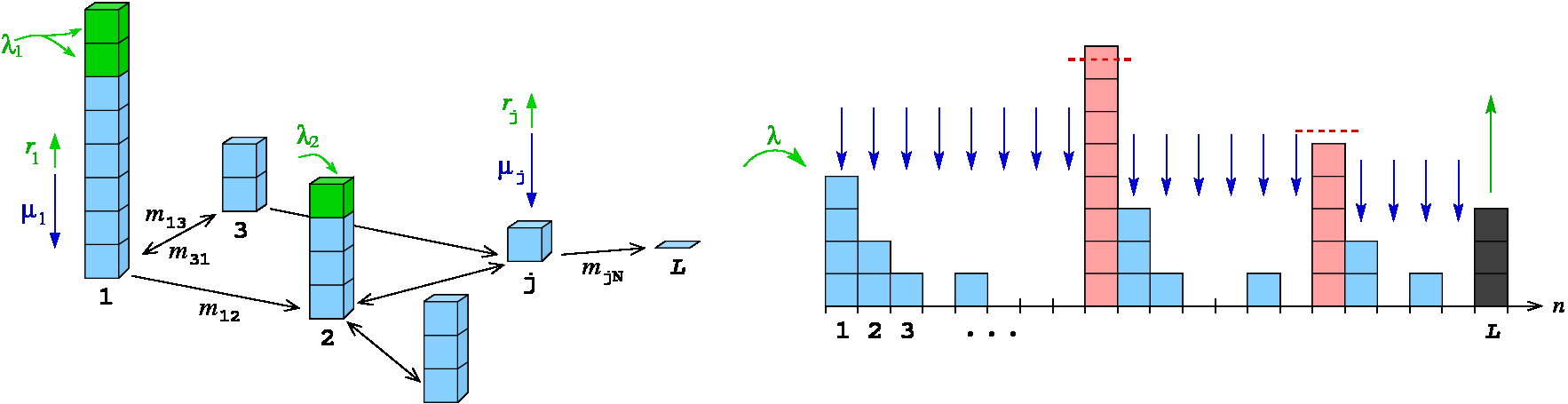
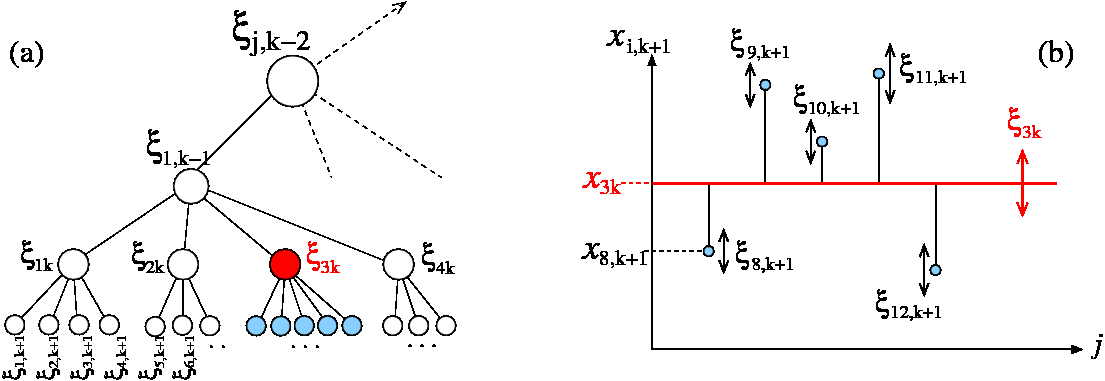
Stochastic models of cellular evolution and cancer progression Our group is currently developing more rigorous models of evolution by analyzing discrete lattice models of birth-death processes that incorporate different modes of mutation, including both spontaneous somatic mutations, and proliferation-induced mutations. Using techniques for exactly and asymptotically analyzing the associated multi-dimensional generating functions, we have found significant qualitative differences between Fokker-Planck treatments and our fully discrete models, particularly with respect to the first passage time distribution of the appearance of a cell containing a fixed number of mutations. We are keen to expand these ideas to models of cancer progression, stem cell aging, as well as more theoretical investigations into hierarchically-coupled stochastic processes.
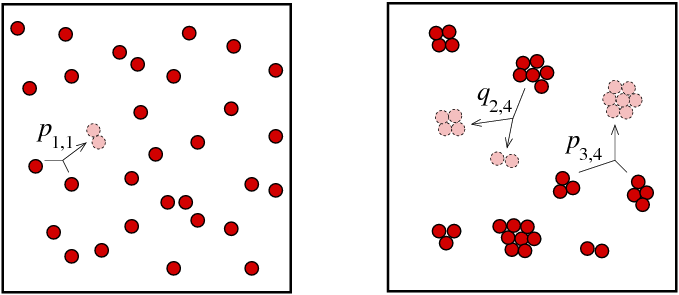
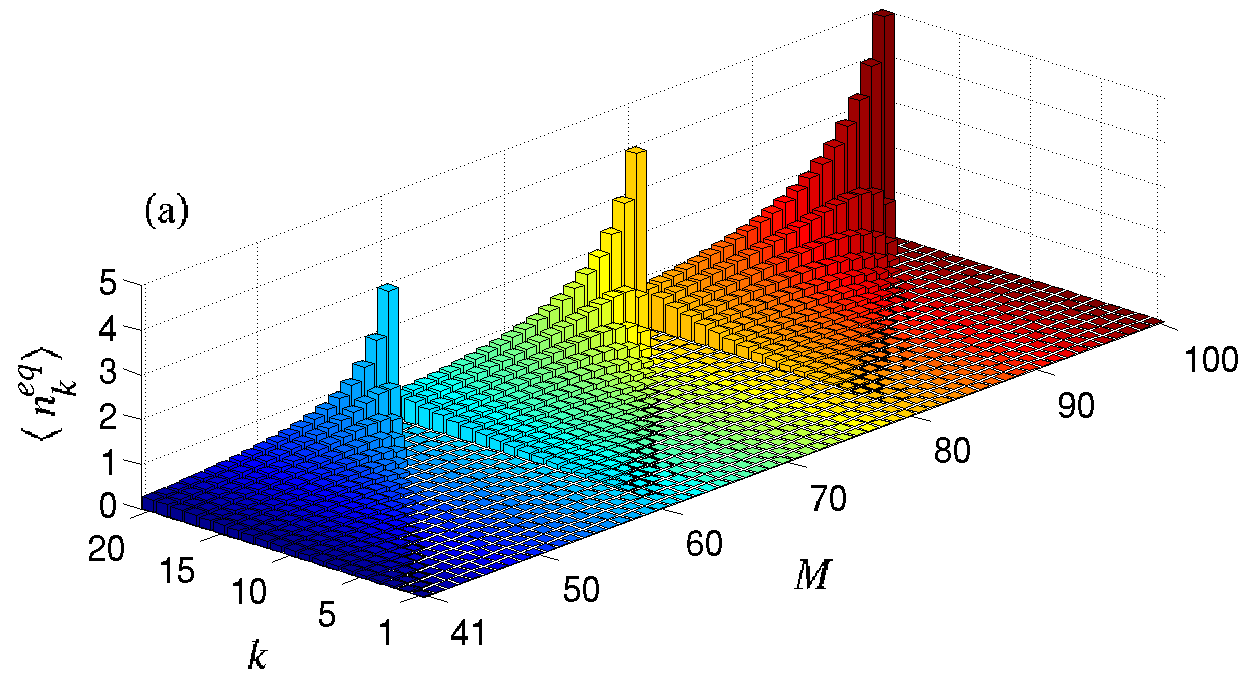
Stochastic nucleation and self-assembly My collaborators and I have developed new stochastic models for nucleation and self-assembly in finite systems. Most recently, we have found a new regime for which classic Becker-Doring mass-action fails to qualitatively describe cluster distributions. We found incommensurate masses that allow a dramatic broadening of the cluster size distribution. This emulsification effect arises from an entropically-driven proliferation of the number of lowest free energy configurations that carry near-uniform cluster size distributions. These results are being extended to include heterogeneous self-assembly mechanisms, and more complicated particle attachment and detachment rules. Finally, we are also combining simulational, combinatoric, and asymptotic methods to compute the first assembly time distributions for clusters of a certain size. These distributions describe the time to completion of a self-assembly process such as virus capsid assembly or membrane pore formation.
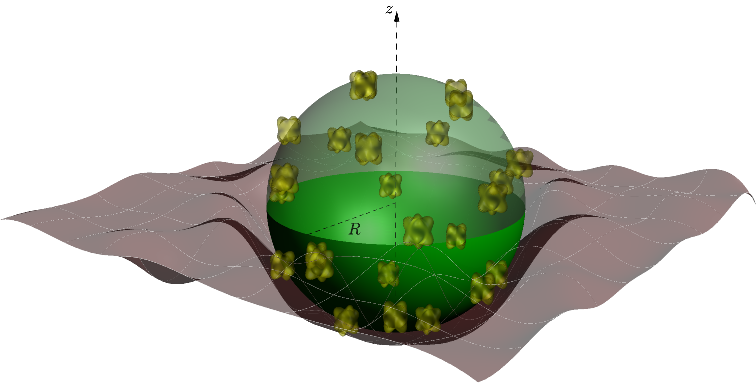
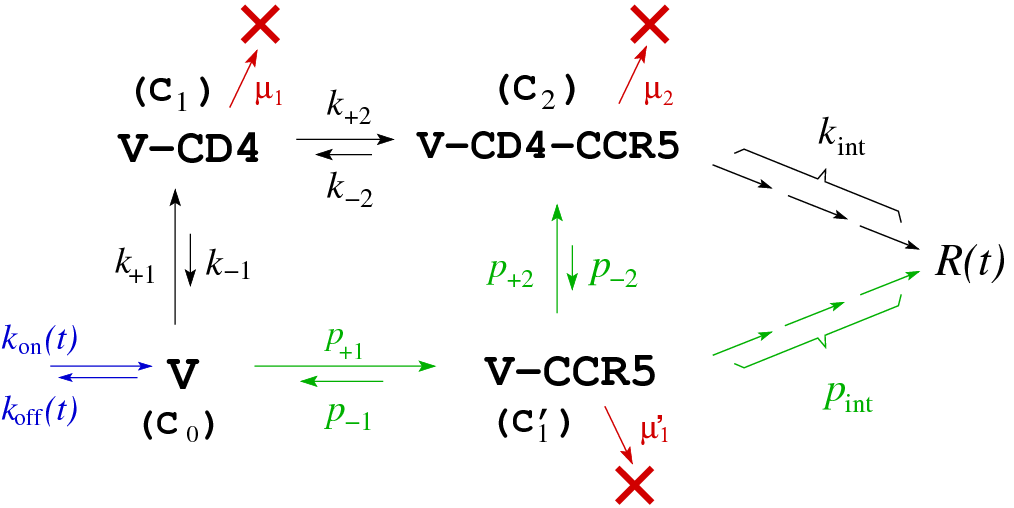
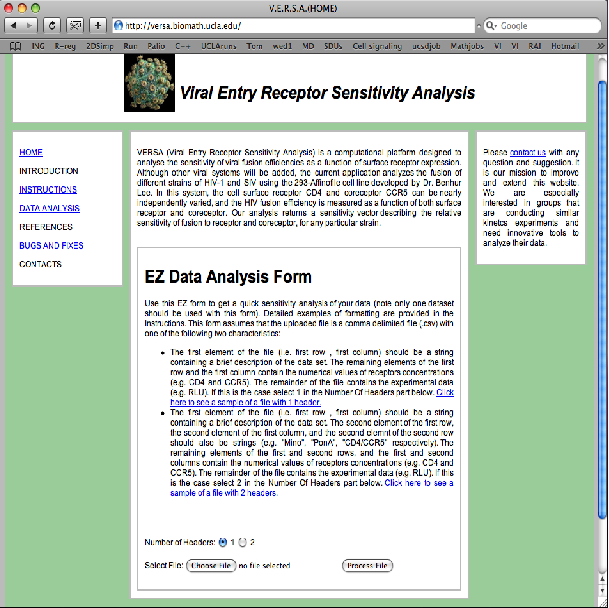
Data analysis for viral infectivity assays In collaboration with Prof. Benhur Lee (MSSM), we are devloping assays to quantify viral infectivity. We are using high-throughput data to inform the development of hybrid mechanistic and statistical models for viral entry, specifically HIV-1. The assay we have developed (patent pending) utilizes the 293-Affinofile cell line in which the expressions of CD4 receptor and CCR5 coreceptor can be independently controlled. Measured infectivities are sensitive to exposure protocol (spinoculation), the mechanism of readout, as well as viral strains. We wish to quantitatively isolate the strain-dependence of infectivity through mathematical moldeing ans statistical clustering of data. To more efficiently investigate mechanistic models for receptor/coreceptor engagement, we have developed a web-based data analysis tool VERSA (Viral Entry Receptor Sensitivity Analysis) versa.biomath.ucla.edu. This analysis tool will be significantly improved to include kinetic-parameter estimation and other statistical functionality.
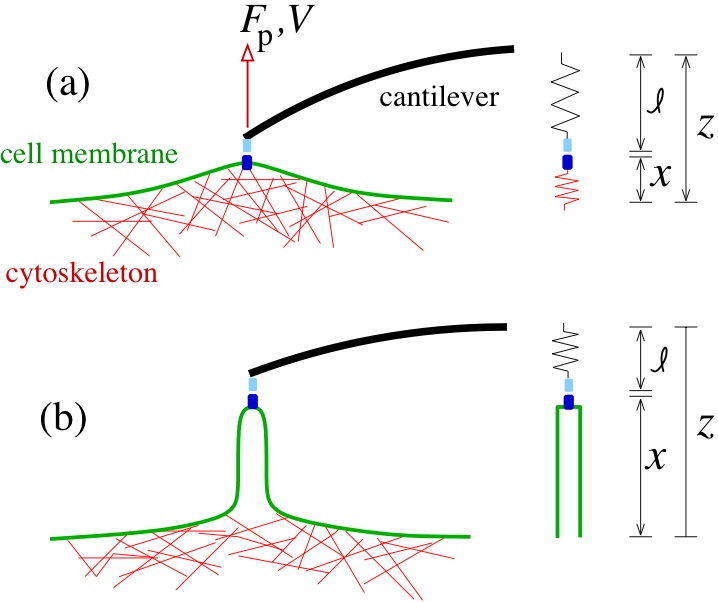
Membrane biophysics The mechanics and dynamics of lipid membranes play a key role cell function. However, the richness in their function derives from their interactions with embedded membrane proteins, the surrounding cytoskeleton, and other particles. My group has developed and carefully analyzed mathematical models describing membrane protein-protein interactions, adhesion-mediated endocytosis, and membrane delamination from cytoskeleton.
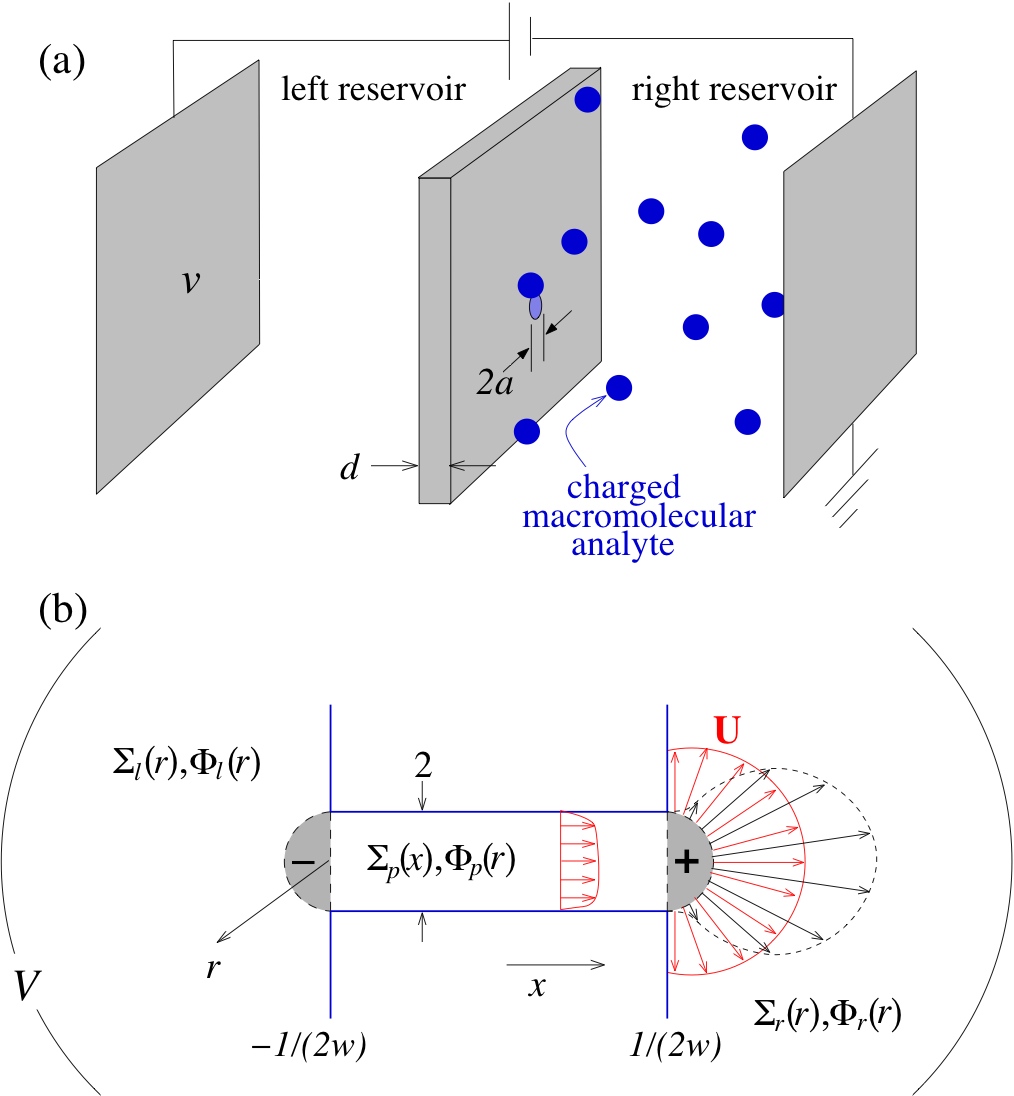
Electrostatics and electrokinetics The goal of this research is to use variational methods to solve particular problems in electrostatics and electrokinetics. We have derived an effective Young-Dupre equation describing the contact angle of an electrolytic droplet in contact with an ionizable surface. We have also found the lowest order solution in the infinitely conducting fluid limit of electrokinetic flow across nanopore. This electrokinetic flow can affect the capture rate of charge macromolecules to the pore in unexpected ways.
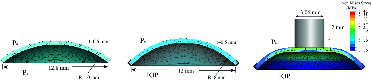
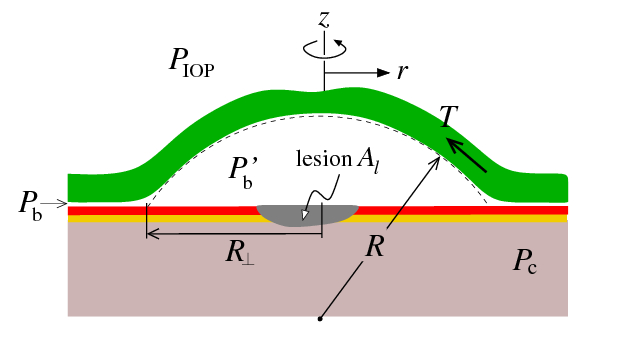
Cornea mechanics and retinal detachment The measurement of intraocular pressure (IOP), considered a key risk factor in the development of glaucoma, is typically measured using very crude indentation devices that are calibrated to a single model system. Individual characteristics are not accounted for and the measured, apparent IOP may be different from the true IOP. We are developing the appropriate shell theory to account for the effects of corneal bending forces on IOP measurement. Another interesting aspect of this problem is how anterior fluid flow affects the measured IOP. We have also developed mechanical models for exudative retinal detachments that include forces from retinal adhesion, retinal pigment epithelium pumps, and retinal elasticity. Regimes for unstable, stable, or self-healing blisters have been delineated. Possible extensions to epithelial wounds and skin blisters are being explored.
