Problem E-1. Prove the half-way-point property of Bézier curves.
Problem E-2. (a) Find the coordinate functions of the Bézier curve with control points (0,0), (1,0), (1,1), (0,2). (b) Sketch this curve. (Instead of plotting many points, it is usually better to plot a few points and find the tangent vectors there to tell the direction of the curve.)
Problem
E-3. Here is a graphical construction of a cubic
Bézier curve: For each ![]() value you want, first mark
the point corresponding to
value you want, first mark
the point corresponding to ![]() on each segment
on each segment
![]() ,
,
![]() , and
, and
![]() . Call the resulting points
. Call the resulting points ![]() ,
,
![]() ,
, ![]() . (For example, if
. (For example, if
![]() , each
, each ![]() is the midpoint of its segment.) Then
mark the point corresponding to
is the midpoint of its segment.) Then
mark the point corresponding to ![]() on
on
![]() and
and
![]() . Call the resulting
points
. Call the resulting
points ![]() ,
, ![]() . Finally mark the point
corresponding to
. Finally mark the point
corresponding to ![]() on
on
![]() . Call
the resulting point
. Call
the resulting point ![]() . Then
. Then
![]() .
.
(a) Carry out this construction for the control points in
Problem E-![]() , for the cases
, for the cases ![]() ,
, ![]() ,
, ![]() .
.
(b) Prove algebraically that the construction works.
(Express the ![]() ,
, ![]() and
and ![]() in terms of
in terms of
![]() and the
and the ![]() , and simplify.)
, and simplify.)
(c) Prove the Half-way Point property by reasoning graphically--why
does the point
![]() come out three-quarters of the way from
the midpoint of
come out three-quarters of the way from
the midpoint of
![]() to the midpoint of
to the midpoint of
![]() ?
?
Problem E-4. Which of the properties listed for the cubic Bernstein polynomials are fairly evident from the graphs shown, and which are not as evident?
Problem E-5. Prove the unit sum property of the cubic Bernstein polynomials.
Problem
E-6. Prove the values given for the first and second
derivatives of the cubic Bernstein polynomials at ![]() and
and ![]() .
.
Problem
E-7. Prove the maximum property for the cubic
Bernstein polynomials. (Do derivatives help for all ![]() ?)
?)
Problem
E-8. Prove the linear sum property for the cubic
Bernstein polynomials. (One way: First consider just the
case where
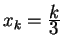 for
for
![]() .
The general case follows from this case and the unit sum
property.)
.
The general case follows from this case and the unit sum
property.)
Problem E-9. Prove the basis property for the cubic Bernstein polynomials.
(Since the dimension of the vector space is known to be
four, it is enough to show either that the cubic Bernstein
polynomials span the vector space or that they are
linearly independent. For the first way: Show how to
express each of
![]() as a linear combination
of cubic Bernstein polynomials. For the second way: Given
a linear combination that is the zero function, i.e., is
zero for all values of
as a linear combination
of cubic Bernstein polynomials. For the second way: Given
a linear combination that is the zero function, i.e., is
zero for all values of ![]() , look at the values of the
linear combination at
, look at the values of the
linear combination at ![]() and at
and at ![]() and
also the values of the first derivative at the same places.)
and
also the values of the first derivative at the same places.)
Problem
E-10. Give an example of a ``cubic'' Bézier curve
(using the ![]() ) that actually has (a) degree 1;
(b) degree 0; (c) degree 2. (Recall that the degree of
a polynomial parametric curve is the maximum of the degrees
of its coordinate polynomials.)
) that actually has (a) degree 1;
(b) degree 0; (c) degree 2. (Recall that the degree of
a polynomial parametric curve is the maximum of the degrees
of its coordinate polynomials.)
Problem
E-11. For cubic Bézier curves, verify (a) the
formulas for the first derivatives at ![]() and
and ![]() ; (b) the formulas for the second derivatives at
; (b) the formulas for the second derivatives at ![]() and
and ![]() ; (c) the tangency property (by using
(a)). (You may quote any relevant properties of cubic
Bernstein polynomials.)
; (c) the tangency property (by using
(a)). (You may quote any relevant properties of cubic
Bernstein polynomials.)
Problem
E-12. Prove this version of Taylor's Theorem for cubic
Bézier curves:
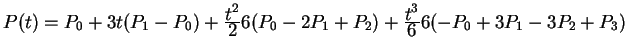 . (One method: algebraic expansion.
Another method: Verify that both sides have the same values
and first, second, and third derivatives at
. (One method: algebraic expansion.
Another method: Verify that both sides have the same values
and first, second, and third derivatives at ![]() ,
because then by the regular Taylor's Theorem they must have
the same cubic polynomials for each coordinate.)
,
because then by the regular Taylor's Theorem they must have
the same cubic polynomials for each coordinate.)
Problem E-13. Prove the convex hull property of cubic Bézier curves. (You may quote any needed properties of convex combinations and of cubic Bernstein polynomials.)
Problem
E-14. If the four control points for a cubic Bézier
curve are all equal, then ![]() is constant. Prove
this fact two ways: (a) Using the convex hull property of
cubic Bézier curves; and (b) using the unit sum property
of Bernstein polynomials.
is constant. Prove
this fact two ways: (a) Using the convex hull property of
cubic Bézier curves; and (b) using the unit sum property
of Bernstein polynomials.
Problem E-15. Consider the affine compatibility property of cubic Bézier curves. On what property of affine transformations and linear combinations does it depend?
Problem
E-16. (a) In pictures of examples like those of
Section 1, why is it acceptable not to indicate the ![]() and
and ![]() axes and a scale? (b) Why is it acceptable not
to indicate which end of the curve has
axes and a scale? (b) Why is it acceptable not
to indicate which end of the curve has ![]() ? (You
may quote relevant properties of Bézier curves, if you
explain how they apply.)
? (You
may quote relevant properties of Bézier curves, if you
explain how they apply.)
Problem E-17. Prove the property of Bézier curves with evenly spaced control points. (You may quote any relevant properties of cubic Bernstein polynomials.)
Problem
E-18. Find the coordinate functions of the Bézier
curve ![]() for the control points
for the control points
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . (Do not attempt a long algebraic method;
instead, quote any relevant properties of Bézier curves.)
. (Do not attempt a long algebraic method;
instead, quote any relevant properties of Bézier curves.)
Problem
E-19. In the upper left diagram in Figure ![]() ,
indicate the point on the curve where each of the two
non-end control points has its maximum influence. (Trace
the curve and control polygon, regard the vertices as the
vertices of the unit square, calculate the two points of
maximum influence, and indicate them.)
,
indicate the point on the curve where each of the two
non-end control points has its maximum influence. (Trace
the curve and control polygon, regard the vertices as the
vertices of the unit square, calculate the two points of
maximum influence, and indicate them.)
Problem
E-20. For an unspecified positive constant ![]() ,
consider the loop made by taking a Bézier curve with
control points
,
consider the loop made by taking a Bézier curve with
control points ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (a) Find
. (a) Find
![]() . (b) Find the
value of
. (b) Find the
value of ![]() at which the
at which the ![]() coordinate is largest,
and the corresponding point on the curve. (c) For what
value of
coordinate is largest,
and the corresponding point on the curve. (c) For what
value of ![]() would the loop just fit inside a unit
square?
would the loop just fit inside a unit
square?
Problem
E-21. (a) Find control points for a cubic Bézier
curve that has exactly the same shape as the arc in Example
2 of Section 5, but goes from ![]() to
to ![]() .
(b) Find points that give an arrowhead so that the whole
curved arrow has exactly the same shape as the one in
Example 3 of Section 5.
.
(b) Find points that give an arrowhead so that the whole
curved arrow has exactly the same shape as the one in
Example 3 of Section 5.
Problem E-22. Prove the formulas given for finding Bézier control points from Hermite data.
Problem
E-23. Sketch a cubic parametric curve ![]() such
that
such
that ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() , and
, and ![]()
![]()
![]() .
.
Problem E-24. Prove the algebraic generality property of cubic Bézier curves.
(Method: Write
![]() . You may quote
the ``basis'' property of Bernstein polynomials. A suitable
linear combination of them gives the
. You may quote
the ``basis'' property of Bernstein polynomials. A suitable
linear combination of them gives the ![]() , and
similarly for
, and
similarly for ![]() . How should you choose the control
points?)
. How should you choose the control
points?)
Problem E-25. Prove the geometric generality property of cubic Bézier curves.
(Method: The difference from the algebraic generality
property is that you must consider any segment of a cubic
parametric curve, not just the segment
![]() . Accordingly, suppose
. Accordingly, suppose ![]() is a cubic parametric
curve and consider a segment given by
is a cubic parametric
curve and consider a segment given by
![]() .
Say how to make a re-parameterization
.
Say how to make a re-parameterization ![]() that gives
the same points but for which the same segment is given by
that gives
the same points but for which the same segment is given by
![]() . Then use the algebraic generality
property.)
. Then use the algebraic generality
property.)
Problem
E-26. (a) Prove this derivative property of Bernstein polynomials:
![]() , except that a term is omitted if its second
subscript is out of bounds; specifically,
, except that a term is omitted if its second
subscript is out of bounds; specifically,
![]() and
and
![]() are omitted.
are omitted.
(Method: You will need the fact that
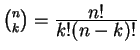 .
Discuss separately the end cases with omitted terms.)
.
Discuss separately the end cases with omitted terms.)
(b) Prove the ``derivative property at any point'' for Bézier
curves of any degree, as given in Section ![]() .
.
(c) Use the derivative property at any point to prove the derivative
properties listed in Section ![]() for cubic Bézier curves.
for cubic Bézier curves.
Problem
E-27. (a) Starting from the fact that
![]() , invent the quadratic Bernstein polynomials
and define quadratic Bézier curves (using three control
points). (b) Sketch the quadratic Bézier curve with
control points
, invent the quadratic Bernstein polynomials
and define quadratic Bézier curves (using three control
points). (b) Sketch the quadratic Bézier curve with
control points ![]() ,
, ![]() ,
, ![]() for
for
![]() . (c) Extend your sketch to
. (c) Extend your sketch to
![]() .
.
Problem
E-28. Show that in
R![]() any quadratic Bézier
curve with noncollinear control points can be mapped onto
any other quadratic Bézier curve with non-collinear
control points by a suitable affine transformation, so that
the control polygon of the first is mapped onto the control
polygon of the second.
any quadratic Bézier
curve with noncollinear control points can be mapped onto
any other quadratic Bézier curve with non-collinear
control points by a suitable affine transformation, so that
the control polygon of the first is mapped onto the control
polygon of the second.
(``Noncollinear'' means ``not in a straight line''. You may assume
any needed properties of quadratic Bézier curves that are
similar to properties of cubic Bézier curves. These curves are
parabolas (unless they are lines), so this problem says that
arbitrary parabolas can be taken to arbitrary parabolas by an
affine transformation, but it says more: This can be done so
that the ![]() values match up, with
values match up, with ![]() on one curve
going to
on one curve
going to ![]() on the other for every
on the other for every ![]() .)
.)
Problem
E-29. Find the coordinate functions ![]() ,
,
![]() ,
, ![]() of a Bézier curve in
R
of a Bézier curve in
R![]() with control
points
with control
points ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Problem
E-30. Show that in
R![]() , any nonplanar cubic
Bézier curve can be mapped by an affine transformation to
any other nonplanar Bézier curve. (You may quote any
relevant properties of Bézier curves.)
, any nonplanar cubic
Bézier curve can be mapped by an affine transformation to
any other nonplanar Bézier curve. (You may quote any
relevant properties of Bézier curves.)
Problem
E-31. Show that as a parametric function of ![]() ,
the first derivative of the cubic Bézier curve with
control points
,
the first derivative of the cubic Bézier curve with
control points
![]() is the same as the
quadratic Bézier curve with control points
is the same as the
quadratic Bézier curve with control points
![]() ,
,
![]() , and
, and
![]() . (One method:
Expand both sides. Another method: Verify that both sides
have the same values and first, second, and third
derivatives at
. (One method:
Expand both sides. Another method: Verify that both sides
have the same values and first, second, and third
derivatives at ![]() , because then by Taylor's Theorem
they must have the same cubic polynomials for each
coordinate.)
, because then by Taylor's Theorem
they must have the same cubic polynomials for each
coordinate.)
Problem
E-32. A certain machine tool is programmed to follow a
cubic Bézier curve in
R![]() . However, it is not
necessarily at point
. However, it is not
necessarily at point ![]() at time
at time ![]() . Instead,
the
. Instead,
the ![]() and
and ![]() coordinates are driven by separate
identical motors and there is a maximum rate at which each
motor can go. Therefore the machine is programmed so that
at any moment either the
coordinates are driven by separate
identical motors and there is a maximum rate at which each
motor can go. Therefore the machine is programmed so that
at any moment either the ![]() motor or the
motor or the ![]() motor
is going at its maximum speed, whether forwards or
backwards. For example, it might be that for the points
with
motor
is going at its maximum speed, whether forwards or
backwards. For example, it might be that for the points
with
![]() on the curve, the
on the curve, the ![]() motor
is at its maximum rate, then for
motor
is at its maximum rate, then for
![]() ,
the
,
the ![]() motor is at its maximum rate, and then for
motor is at its maximum rate, and then for
![]() the
the ![]() motor is at its maximum
rate again. In this example, there were three ranges of
motor is at its maximum
rate again. In this example, there were three ranges of ![]() . Find the maximum number of ranges there could be for
a cubic Bézier curve in general.
. Find the maximum number of ranges there could be for
a cubic Bézier curve in general.
(Method: Imagine the path in
R![]() of the velocity
vector
of the velocity
vector ![]() . By Problem E-
. By Problem E-![]() , this curve is
a quadratic Bézier curve itself. By an earlier problem,
the graph is a parabola. In which regions of
R
, this curve is
a quadratic Bézier curve itself. By an earlier problem,
the graph is a parabola. In which regions of
R![]() is
the
is
the ![]() -motor limiting, and in which regions is the
-motor limiting, and in which regions is the ![]() -motor limiting? Into how many pieces could the curve be
broken by these regions?)
-motor limiting? Into how many pieces could the curve be
broken by these regions?)
Problem E-33. For given Hermite data, is there necessarily a quadratic Bézier curve that satisfies the data? (Either give a method or give a counterexample.)
Problem
E-34. (a) Invent a ``half-way derivative'' property for cubic
Bézier curves, by expressing
![]() in terms of the
control points and looking for a geometrical interpretation.
(It will involve a vector between midpoints of two sides of
the control polygon, times a factor.)
in terms of the
control points and looking for a geometrical interpretation.
(It will involve a vector between midpoints of two sides of
the control polygon, times a factor.)
(b) Show that at
![]() the curve is parallel to the line segment
joining the midpoints of the first and last legs of the control
polygon.
the curve is parallel to the line segment
joining the midpoints of the first and last legs of the control
polygon.
Problem E-35. When we say a ``cubic'' Bézier curve we really mean a Bézier curve with four control points and of degree at most 3. Invent a criterion for a cubic Bézier curve to have degree at most two. Express your criterion in terms of the control points. If possible, given a pictorial interpretation.
(Method: A curve is quadratic when its third derivative is always zero. Analogously to the ``Second derivative at ends'' property, derive a ``Third derivative at ends'' property. Actually, since the third derivative of a cubic function is constant, the third derivative will be the same at both ends and everywhere else. Now set the third derivative = 0.)
Problem
E-36. For each graph in Figure ![]() ,
do the following, separately for each:
Choose
,
do the following, separately for each:
Choose ![]() -axes so that the lower-left vertex is at
the origin and so that all control points have integer
coordinates, with all their coordinates together having greatest
common divisor 1. Then calculate
-axes so that the lower-left vertex is at
the origin and so that all control points have integer
coordinates, with all their coordinates together having greatest
common divisor 1. Then calculate
![]() in decimals,
and see if it does seem to match the graph.
in decimals,
and see if it does seem to match the graph.
Problem
E-37. Plot the following functions together on one graph,
for
![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Problem
E-38. On a single graph, plot the Bézier curve with
control points ![]() ,
,
![]() ,
,
![]() ,
, ![]() and also the three other Bézier curves whose control points are
the same as these times
and also the three other Bézier curves whose control points are
the same as these times
![]() ,
,
![]() ,
and
,
and
![]() , respectively. This gives a pretty good
approximation to a circle.
, respectively. This gives a pretty good
approximation to a circle.
Problem
E-39. For a Bézier curve of degree 4, with control
points
![]() , invent a Half-way Point Property
in terms of
, invent a Half-way Point Property
in terms of ![]() and the midpoints of
and the midpoints of
![]() and
and
![]() .
.
Problem
E-40. Sketch a parametric cubic curve ![]() for which
for which
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Problem
E-41. Show that for a cubic Bézier curve with control points
![]() ,
, ![]() ,
, ![]() ,
, ![]() , the center of
mass of the ``control triangle'' for
, the center of
mass of the ``control triangle'' for ![]() is the same as
the ``missing leg''
is the same as
the ``missing leg''
![]() (as a vector) in the
original control polygon. (You may quote the result of Problem E-
(as a vector) in the
original control polygon. (You may quote the result of Problem E-![]() .)
.)
Problem
E-42. Find the set of ![]() with
with
![]() for which
for which
![]() has the largest value among the four Bernstein
polynomials of degree 3. This is the same as the set of
has the largest value among the four Bernstein
polynomials of degree 3. This is the same as the set of ![]() for which
for which ![]() has the largest influence among the four
control points. Correspondingly, where does each of
has the largest influence among the four
control points. Correspondingly, where does each of ![]() ,
, ![]() , and
, and ![]() have the largest influence, in
terms of sets of
have the largest influence, in
terms of sets of ![]() ?
?