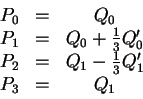The control points in this example are ![]() ,
,
![]() ,
, ![]() ,
, ![]() . If you
instead want an arc of this exact shape between other given
points
. If you
instead want an arc of this exact shape between other given
points ![]() and
and ![]() , find an affine matrix that
does a rotation, uniform scaling, and translation to move
the segment
, find an affine matrix that
does a rotation, uniform scaling, and translation to move
the segment
![]() to
to
![]() . To do this, write
. To do this, write
![]() and
and
![]() and then use the extended matrix
and then use the extended matrix
![$ {\left[\begin{array}{rrr}a&b&0\\ -b&a&0\\ c&d&1\end{array}\right]} $](img97.gif) .
.
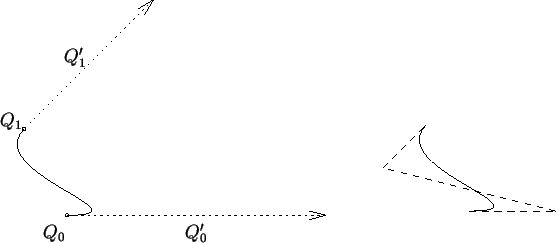
A solution is to use a Bézier curve with
appropriate control points ![]() ,
, ![]() ,
, ![]() ,
,
![]() . As you see,
. As you see, ![]()
![]()
![]() and
and ![]()
![]()
![]() . Also, from the first derivative
property,
. Also, from the first derivative
property,
![]()
![]()
![]() and
and
![]()
![]()
![]() . These last two equations can
be solved for
. These last two equations can
be solved for ![]() and
and ![]() . We get these
Bézier control points, as shown in the right-hand portion
of Figure
. We get these
Bézier control points, as shown in the right-hand portion
of Figure ![]() .
.