


Next: e_bezier
Up: e_bezier
Previous: e_bezier
3. Some properties of cubic Bézier curves
Let 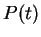 be the Bézier curve with four
control points
be the Bézier curve with four
control points 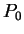 ,
, 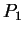 ,
, 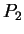 ,
, 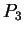 .
.
- Degree:
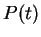 has degree at most
has degree at most 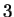 (one
less than the number of control points).
(one
less than the number of control points).
- Special values:
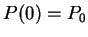 ,
,
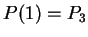 .
.
- Tangency: At
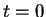 the Bézier curve is
tangent to the first leg of its control polygon; at
the Bézier curve is
tangent to the first leg of its control polygon; at 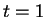 it is tangent to the last leg.
it is tangent to the last leg.
- Convex hull: For
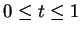 , the Bézier
curve lies entirely in the convex hull of its control
points.
, the Bézier
curve lies entirely in the convex hull of its control
points.
- First derivative at ends:
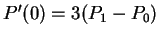 and
and
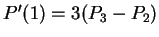 .
.
- Second derivative at ends:
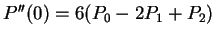 and
and
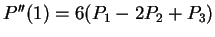 .
.
- Affine compatibility: The Bézier construction is
compatible with affine transformations
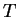 . In other
words,
. In other
words, 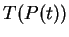 is the same as the point at time
is the same as the point at time 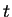 on the Bézier curve with control points
on the Bézier curve with control points 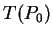 ,
,
 ,
, 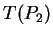 ,
,  .
.
- Evenly spaced control points: If
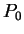 ,
, 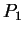 ,
, 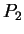 ,
, 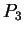 are evenly spaced along a straight
line, then
are evenly spaced along a straight
line, then 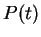 reduces to the usual parametric form
of a line segment, namely
reduces to the usual parametric form
of a line segment, namely
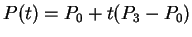 .
.
- Maximum influence: For
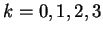 , the control
point
, the control
point 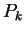 has its maximum influence (i.e., its
coefficient is at a maximum) at time
has its maximum influence (i.e., its
coefficient is at a maximum) at time
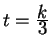 .
.
- Symmetry:
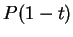 is the same as the Bézier
curve with control points in the opposite order:
is the same as the Bézier
curve with control points in the opposite order: 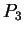 ,
,
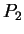 ,
, 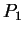 ,
, 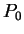 .
.
- Half-way point:
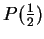 is
is
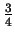 of the way from the midpoint of the segment
of the way from the midpoint of the segment
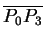 to the midpoint of the segment
to the midpoint of the segment
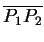 .
.
- Generality, algebraically: For any cubic parametric
curve
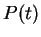 , its portion
, its portion
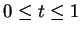 is a
Bézier curve, for suitable chosen control points.
is a
Bézier curve, for suitable chosen control points.
- Generality, geometrically: Any segment of a cubic
parametric curve has the same points as some Bézier curve
(with suitably chosen control points).



Next: e_bezier
Up: e_bezier
Previous: e_bezier
Kirby A. Baker
2003-04-04
![]() be the Bézier curve with four
control points
be the Bézier curve with four
control points ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
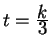 .
.