8. Problems

Problem X-1. Write Examples and in coordinate form. (For the coordinates of the given points, just write $P_i = (x_i, y_i)$.)

Problem X-2. For the (non-polynomial) parametric curve $P(t) = (\cos t, \sin t)$, sketch the curve, the graph of $x$ against $t$, and the graph of $y$ against $t$, for $-\pi \leq t \leq 3 \pi$.

Problem X-3. Find $P (t)$ explicitly in the upper right example of Figure , by using basis functions. Assume that the data points are $P_0 = (0,0)$, $P_1 = (1,0)$, $P_2 = (1,1)$, and $P_3 = (2,1)$, with $t_i = i$ for $i = 0,1,2,3$.

Problem X-4. Find a quadratic polynomial curve $P (t)$ (or really, a polynomial curve $P (t)$ of degree at most two) such that $P(-1) = (1,5)$, $P(0) = (2,1)$, and $P(1) = (3,5)$, by using basis functions. Give explicit coordinate functions $x(t)$, $y(t)$.

Problem X-5. Find a cubic polynomial curve $P (t)$ (or really, a polynomial curve $P (t)$ of degree at most three) such that $P(0) = (1,0)$, $P(1) = (2,1)$, $P(2) = (9,2)$, and $P(3) = (28,3)$. Use basis functions.

Problem X-6. Solve Problem X- using divided differences.

Problem X-7. Suppose that you want to make a parametric curve $P (t)$, polynomial or not, to interpolate data points $P_i$ with $P(t _ i) = P _ i$ for $i = 0,\dots, n$, and suppose that you plan to express $P (t)$ as a linear combination with time-varying coefficients. What conditions on the blending functions (the coefficient functions) are sufficient to guarantee that $P (t)$ does interpolate as required?

Problem X-8. Find the Lagrange blending functions of degree one.

Problem X-9. (a) Find a quadratic parametric curve that crosses the unit circle $x^2 + y^2 = 1$ in four points. (b) Find a cubic parametric curve that crosses the unit circle in six points. (In both parts, the equations should be explicit but a graphical proof is sufficient. One method for (b): If you can find a suitable graph $y = a x^3 + b x^2 + c x + d$, you can express the same graph in parametric form as $(t, a t^3 + \dots + d)$.)

Problem X-10. Show that the unit circle $x^2 + y^2 = 1$ cannot be represented as a polynomial parametric curve. In fact, show that a polynomial parametric curve of degree $n>0$ cannot touch a unit circle in more than $2n$ distinct points, much less follow the circle all the way around. For example, a parabola cannot touch a circle in more than four points.

(Method: Suppose the curve is $P(t) = (x(t), y(t))$ of degree $n$. For any $t$ for which $P (t)$ is on the circle, we get $x(t)^2 + y(t)^2 = 1$. Apply the agreement property of polynomials from § to show that if more than $2n$ points of the curve are on the circle, then all points of the curve are on the circle. Apply the unboundedness property from § to show that this is impossible. Then you have made a proof by contradiction.)

Problem X-11. (a) In contrast to the preceding problem, show that the following method does give a parametrization of the unit circle (except for one point) by rational functions (ratios of polymials): Calculate the point $(x,y)$ where the line of slope $m$ through the point $(-1,0)$ on the circle intersects the circle a second time. Your answer will have $x$ and $y$ as rational functions of $m$, say $x(m)$ and $y(m)$. Now write $t$ for $m$, to use a more familiar parameter. Check that $x(t)^2 + y(t)^2$ is always 1.

(b) Which point of the circle is missing?

(c) Try some rational-number values for $t$; the corresponding $x$ and $y$ should lead to some ``Pythagorean triples'' such as $3,4,5$ with $3^2 + 4^2 = 5^2$ and $5,12,13$ with $5^2 + 12^2 = 13^2$. Reduce each triple you get to lowest terms, e.g., use $3,4,5$ and not $6,8,10$. Find three triples in lowest terms other than the ones just mentioned.

Problem X-12. Suppose that you have chosen a list $f_0 (t),\dots, f_n (t)$ of blending functions, not necessarily polynomials, for which $f_0 (t) + \dots + f_n (t) = 1$ for all $t$ with $a \leq t \leq b$. Then given a list of points $P_0,\dots, P_n$ you can make a curve by using the functions $f_i (t)$ as coefficients of a linear combination $P (t)$ $=$ $f_0 (t) P_0 + \dots + f_n (t) P_n$. Explain how you know that this process is compatible with affine transformations. In other words, show that if $T$ is an affine transformation and $Q_i = T(P_i)$ for each $i$, then at all times $t$ with $a \leq t \leq b$ you get $T(P(t)) = Q(t)$, where $Q(t)$ is the curve made with the same blending functions but based on the points $Q_i$. (Method: What property of affine transformations and linear combinations is relevant?)

Problem X-13. A useful observation is that a polynomial, say $1 + 2t + 7t^2 - 5 t^3$, can be written as a matrix product ${\left[\begin{array}{cccc} 1&t&t ^ 2&t ^ 3\end{array}\right]} {\left[\begin{array}{c}1\\ 2\\ 7\\ -5\end{array}\right]}$.

Similarly, the polynomial curve $(1 + 2t + 7t^2 - 5 t^3,4 - t + t^2)$ can be written as ${\left[\begin{array}{cccc}1&t&t ^ 2& t ^ 3\end{array}\right]} {\left[\begin{array}{cc}1&4\\ 2&-1\\ 7&1\\ -5&0\end{array}\right]}$.

As you see, the columns of the right-hand matrix represent the coefficients of the $x$ and $y$ coordinate polynomials. (It is usually best to write polynomials in this situation with increasing powers of $t$, although some texts do not.)

Express Example in matrix form.

Problem X-14. Another use of matrices is to make a ``matrix of points'', a matrix in which each row represents a point. For example, if data points $P_0,\dots, P_n$ are given, the corresponding matrix is $P_* = {\left[\begin{array}{c}P _ 0\\ \dots \\ P _ n\end{array}\right]}$. Then a linear combination of these points with blending functions $f_0,\dots, f_n$ can be expressed by the matrix product $P (t)$ $=$ $\left[\begin{array}{ccc}f _ 0 (t)&\dots &f _ n (t)\end{array}\right] P_*$.

(a) Express Example in this form, for the case $P_0 = (7,2)$, $P_1 = (-1,4)$, $P_2 = (3,6)$.

(b) Combine (a) with the method of the preceding problem to write the same example in the form $P(t) = \left[\begin{array}{ccc}1&t&t ^ 2\end{array}\right] M P_*$, where $M$ is a certain matrix of numbers. (Do not multiply out.)

Problem X-15. Complete the details in the proof of Theorem .

Problem X-16. A Van der Monde matrix is a matrix of the form

$$V = {\left[\begin{array}{ccccc} 1&t _ 0&t _ 0 ^ 2&\dots &t _ 0 ^ ... ...dots &\dots &&\dots \\ 1&t _ n&t _ n ^ 2&\dots &t _ n ^ n \end{array}\right]}$$

This matrix is $(n+1) \times (n+1)$. The $t_i$ can be any numbers. For example, ${\left[\begin{array}{ccc}1&2&4\\ 1&3&9\\ 1&\pi& \pi ^ 2\end{array}\right]}$ is a van der Monde matrix.

A theorem is that the determinant of a van der Monde matrix is the product of the 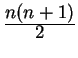${{\frac{\displaystyle n(n+1)}{\displaystyle 2}}}$ terms $(t_j - t_i)$ with $i<j$, or symbolically, $\prod _ {i<j} (t_j - t_i)$. For example, for a $3 \times 3$ van der Monde matrix, the determinant is $(t_1 - t_0) (t_2 - t_0) (t_2 - t_1)$.

(a) Verify this theorem in the case $n = 2$.

(b) Explain why a van der Monde matrix must be nonsingular if the numbers $t_0,\dots, t_n$ are distinct.

(c) Find the volume of the tetrahedron with vertices $(8,8^2,8^3)$, $(9,9^2,9^3)$, $(10,10^2,10^3)$, $(11,11^2,11^3)$, using only arithmetic that is so easy you could do it in your head.

(Method: Recall that the volume can be expressed as ${\frac 1 6}$ of the absolute value of a certain determinant whose last column consists of $1$'s. Changing the order of the columns does not change the absolute value of a determinant.)

Problem X-17. Here is a different approach to solving a Lagrange interpolation problem. As usual, let points $P_i$ in    R$^2$ and distinct times $t_i$ be given, for $i = 0,\dots, n$. According to a preceding problem, a solution can be written in the form $P (t)$ $=$ $\left[\begin{array}{ccccc}1&t&t ^ 2&\dots & t ^ n\end{array}\right] C$, where $C$ is some $(n+1) \times 2$ matrix of coefficients. The interpolation conditions $P(t _ i) = P _ i$ can then be written as $\left[\begin{array}{ccccc}1& t _ i& t _ i ^ 2&\dots &t _ i ^ n\end{array}\right] C$ $=$ $P_i$. These conditions can be combined into a single matrix equation $VC = P_*$, where $V$ is a van der Monde matrix.

(a) Explain why there must be a solution for the matrix $C$ of coefficients and why this solution is unique. (You may quote any needed properties of van der Monde matrices.)

(b) Explain how you could solve Lagrange problems on a computer in this way if a row-reduction routine were available.

Problem X-18. Prove the uniqueness part of Theorem : There is only one polynomial curve $P (t)$ of degree at most $n$ for which $P(t_0) = P_0, \dots, P(t_n) = P_n$, where the $P_i$ and $t_i$ are any given points and distinct times.

(Method: Apply the uniqueness property of § to the coordinate polynomials.)

Problem X-19. Using the ``Agreement in many places'' property in §, explain how you get the (a) the ``Expression from function'' property and (b) the ``Continuation'' property.

Problem X-20. Find an example of a polynomial curve $P (t)$ that goes through data points that are in a rectangular window, such that the curve wanders out of the window between two of the data points.

(You should give explicitly the bounds of the window, the coordinate functions of the curve, and the time at which the curve is outside the window. Such an example will contrast with other kinds of polynomial curves to be studied soon.)

Problem X-21. Consider the Lagrange blending functions $p_0 (t),\dots, p_n (t)$ for given distinct $t_0,\dots, t_n$.

(a) Show that for all $t$, $p_0 (t) + \dots + p_n (t) = 1$.

(b) Show that for all $t$, $t_0 p_0 (t) + t_1 p_1 (t) + \dots + t_n p_n (t) = t$.

(Method: In each case, try to use the agreement property from §, applied to the two sides.)

Problem X-22. Show that the Lagrange blending functions $p_i (t)$ for given distinct $t_0,\dots, t_n$ form a basis for the vector space of all polynomials of degree at most $n$.

(Method #1: Because you already know the vector space has dimension $n+1$, it is enough to show that the $p_i$ are linearly independent. Suppose some linear combination $c_0 p_0 (t) + \dots + c_n p_n (t)$ $=$ $0$, for all $t$. Substitute in various appropriate values of $t$ and see if you can show the $c_i$ are all zero.)

(Method #2: It is also enough to show that any $f$ in the vector space is a linear combination of the polynomials $p_i (t)$. Given $f$, let $c_i = f ( t_i )$ and show that $c_0 p_0 (t) + \dots + c_n p_n (t)$ $=$ $f(t)$ for $n+1$ different values of $t$. Then quote the uniqueness property.)

Problem X-23. This problem shows that a polynomial curve of degree two is a parabola, provided that it does not lie on a straight line.

(a) How can a parabola $y = ax^2 + bx + c$ be expressed parametrically?

(b) Show that a parametric curve of the form $(rt+s,at^2 + bt + c)$ is a parabola, if $r \neq 0$ and $a \neq 0$.

(Method: reparameterize the curve using $u = rt+s$, so $t = \dots$)

(c) What does the graph of the derivative of a parametric curve of the form given in (b) look like? Does the derivative curve go through the origin?

(d) Show that if $P (t)$ is a polynomial curve of degree 2 and the graph of $P'(t)$ does not go through the origin, then $P (t)$ is a parabola.

(Method: $P'(t)$ has degree 1, so is a straight line. If $P'(t)$ does not go through the origin, observe that there is a $2 \times 2$ rotation matrix $R$ which rotates this line to be parallel to the $y$-axis. The rotated curve $P(t)R$ has derivative ...since $R$ is a constant matrix. Integrate to get an expression like that in (b) for $P(t)R$.)

(e) On the other hand, if the graph of $P'(t)$ is a line through the origin, then show that $P (t)$ itself lies on a straight line.

(Method: As in (d), rotate the derivative until its graph is parallel to the $y$-axis, and then integrate.)

Problem X-24. The curve shown in Figure is actually a polynomial curve of degree 5 that solves a Lagrange problem with $t_i = i$ for each $i$. With this information, write down an explicit formula for the curve. (Choose a coordinate system with the origin at the lower left data point. Any scale is acceptable. Do not attempt to simplify your answer.)

Problem X-25. A perfect unit circle can be given parametrically by $P (t)$ $=$ $(\cos t, \sin t)$. Suppose $P_n (t)$ is the parametric curve obtained by using instead the Taylor polynomial approximations to $\cos t$ and $\sin t$ of degree at most $n$. Sketch the curves described by $P_1 (t)$ and $P_2 (t)$. What do you think happens as for larger and larger values of $n$? (Note: Since the Taylor expansion of $\cos t$ has only terms with even powers of $t$, the Taylor polynomials of degrees, say, 8 and 9 are the same. Similarly, the Taylor polynomials for $\sin t$ of degrees 7 and 8 are the same.)

Problem X-26. Suppose the cubic curve $P (t)$ has $P(0) = P_0$, $P(1) = P_1$, $P(2) = P_2$, and $P(3) = P_3$. Since a cubic curve is determined uniquely by interpolating four points at given $t$ values, everything about $P (t)$ should be describable in terms of $P _ 0,\dots, P _ 3$.

(a) Give an expression for $P'(0)$ in terms of $P _ 0,\dots, P _ 3$.

(b) Give an expression for the middle value $P(1.5)$ in terms of $P _ 0,\dots, P _ 3$.

(Method: First use Lagrange to find an explicit expression for $P (t)$ in terms of the $P_i$. Are your answers to (a) and (b) linear in the $P_i$?)

Problem X-27. Show that every plane polynomial curve of degree $k$ has a mirror symmetry (perhaps not through the origin) for

(a) $k=1$,

(b) $k=2$,

(c) $k=3$.