To keep things simple, let's start with the case
where ![]() and
and ![]() ,
, ![]() ,
, ![]() , and let's just try to find
, and let's just try to find ![]() . Thus we
want
. Thus we
want ![]() so that
so that
![]() ,
,
![]() ,
,
![]() .
.
As a first goal, let's just try to make a polynomial
that is zero at ![]() and at
and at ![]() but not at
but not at ![]() . That is easy: The function
. That is easy: The function
![]() works. It is nonzero at
works. It is nonzero at ![]() because the value there
is a product of two nonzero factors.
because the value there
is a product of two nonzero factors.
However, at ![]() the value is
the value is ![]() and
not
and
not ![]() as desired. Fortunately, all we need to do is
to divide the function by the 10 and we're done:
as desired. Fortunately, all we need to do is
to divide the function by the 10 and we're done:
 .
.
To show where this result came from, we could write
![]() as
as
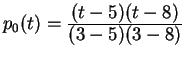 .
.
Now we're ready for ![]() . The same
reasoning gives
. The same
reasoning gives
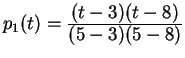 . You can
check that
. You can
check that ![]() at
at
![]() has values
has values ![]() respectively. Similarly,
respectively. Similarly,
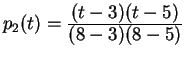 .
.
Now it should be clear how to make ![]() ...,
..., ![]() for general
for general ![]() :
: ![]() is a fraction whose numerator is a product of factors
is a fraction whose numerator is a product of factors ![]() except for
except for ![]() ; the denominator is a
product of the same factors except with
; the denominator is a
product of the same factors except with
![]() instead of
instead of ![]() . To write all this more
compactly, it is handy to use a sign
. To write all this more
compactly, it is handy to use a sign ![]() (capital pi)
for a product, the same way that
(capital pi)
for a product, the same way that ![]() is used for
summation.
is used for
summation.
Theorem 4.1 . The solution to the polynomial interpolation problem can be expressed as
![]() , where for each
, where for each
![]() ,
,
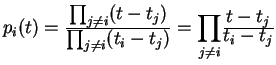 .
.
Proof of Theorem ![]() . Just substitute in
. Just substitute in ![]() , and you will find that each
, and you will find that each ![]() has the right
value, and consequently
has the right
value, and consequently
![]() . Observe that each
. Observe that each ![]() has degree
has degree ![]() . Each coordinate function of
. Each coordinate function of ![]() is a linear combination of
is a linear combination of
![]() and
so has degree at most
and
so has degree at most ![]() .
.
Proof of Theorem ![]() . The existence of the required
solution is shown by Theorem
. The existence of the required
solution is shown by Theorem ![]() . The uniqueness is shown in
the Exercises.
. The uniqueness is shown in
the Exercises.
Note. The polynomials ![]() depend only
on
depend only
on ![]() and the times
and the times
![]() , and not on the
data points
, and not on the
data points ![]() . In Figure
. In Figure ![]() are shown
graphs of the polynomials
are shown
graphs of the polynomials ![]() for
for ![]() and times
and times
![]() .
.