Problem
K-1. Consider the bilinear patch
![]() with corner data
with corner data
![]() ,
,
![]() . Describe the
horizontal cross-section (level curve) for
. Describe the
horizontal cross-section (level curve) for ![]() , and the vertical
cross-section for the plane given by
, and the vertical
cross-section for the plane given by ![]() .
.
Problem
K-2. For the bilinear patch
P![]() with corner data
with corner data ![]() ,
,
![]() ,
, ![]() ,
, ![]() , find a formula for
P
, find a formula for
P![]() .
.
Problem
K-3. For a linearly blended Coons surface
![]() consider
these corner heights and boundary curves:
consider
these corner heights and boundary curves:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() . (a) Is this data consistent?
(b) If it is, find an equation for the surface. (The answer may
be left as a product of matrices.)
. (a) Is this data consistent?
(b) If it is, find an equation for the surface. (The answer may
be left as a product of matrices.)
Problem K-4. Explain in detail why the formula for constructing a parametric Lagrange surface does give the desired interpolation.
Problem
K-5. (a) Explain why a Lagrange surface that has degree 1 in
both ![]() and
and ![]() and has
and has
![]() and
and
![]() is an instance of a bilinear patch (Example 10).
(b) What about a relaxed cubic spline surface, still with
is an instance of a bilinear patch (Example 10).
(b) What about a relaxed cubic spline surface, still with ![]() on both coordinates?
on both coordinates?
Problem
K-6. Here are control points for a Bézier surface with tensor-product
basis, for ![]() . Describe what the surface should look like, either in
words or by an intuitive sketch.
The ``middle four'' control points are the corners of a square in
the
. Describe what the surface should look like, either in
words or by an intuitive sketch.
The ``middle four'' control points are the corners of a square in
the ![]() plane; specifically,
plane; specifically,
![$ P _ {11} = \left[\begin{array}{r}-1\\ -1\\ 1\end{array}\right]$](img168.gif) ,
,
![$ P _ {12} = \left[\begin{array}{r}-1\\ 1\\ 1\end{array}\right]$](img169.gif) ,
,
![$ P _ {21} = \left[\begin{array}{r}1\\ -1\\ 1\end{array}\right]$](img170.gif) ,
,
![$ P _ {22} = \left[\begin{array}{r}1\\ 1\\ 1\end{array}\right]$](img171.gif) . All the other control points are
at the origin.
. All the other control points are
at the origin.
Problem
K-7. Consider the parametric Bézier surface ![]() with
with ![]() and control points
and control points ![]() given by
given by
![$ P _
{ij} = \left[\begin{array}{c}i\\ j\\ 0\end{array}\right]$](img174.gif) except that
except that
![$ P _ {11} = \left[\begin{array}{c}1\\ 1\\ 4\end{array}\right]$](img175.gif) . Since
. Since ![]() , you will need the Bernstein polynomials
, you will need the Bernstein polynomials
![]() ,
,
![]() ,
,
![]() .
.
(a) Find the coordinate functions of ![]() . (Use tensor basis;
simplify algebraically.)
. (Use tensor basis;
simplify algebraically.)
(b) Sketch ![]() . (Just sketch the six isoparametric curves
for
. (Just sketch the six isoparametric curves
for ![]() and
and ![]() values
values ![]() .)
.)
Problem
K-8. Write down an expression for a Lagrange surface with
![]() for the data points
for the data points
![$ P _
{ij} = \left[\begin{array}{c}i\\ j\\ 0\end{array}\right]$](img174.gif) , with
, with ![]() ,
, ![]() , for
, for ![]() and
and ![]() ,
except that
,
except that
![$ P _ {11} = \left[\begin{array}{c}1\\ 1\\ 4\end{array}\right]$](img175.gif) . Then simplify the expression.
(Method: Simplify one coordinate at a time. It can help to use any
properties you know about linear combinations of Lagrange basis functions.
Of course, if you can guess a function that fits the data, then by
the uniqueness of the Lagrange solution that must be correct, so
the algebra is avoided.)
. Then simplify the expression.
(Method: Simplify one coordinate at a time. It can help to use any
properties you know about linear combinations of Lagrange basis functions.
Of course, if you can guess a function that fits the data, then by
the uniqueness of the Lagrange solution that must be correct, so
the algebra is avoided.)
Problem
K-9. Recall that a partial derivative with respect to one
variable is just the derivative when all other variables are held
fixed. For a parametric surface
P![]() , observe that the
two partial derivatives
, observe that the
two partial derivatives
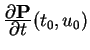 and
and
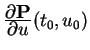 give velocity vectors of the two isoparametric curves at
P
give velocity vectors of the two isoparametric curves at
P![]() . These two vectors are therefore tangent to
the surface, and their cross product is a normal (a
perpendicular) to the surface.
. These two vectors are therefore tangent to
the surface, and their cross product is a normal (a
perpendicular) to the surface.
(a) For the sphere parameterized as
P![$ (t,u) = R _ u ^ {x\rightarrow y} R _ t ^ {x\rightarrow z} \left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$](img42.gif) , or the equivalent written
coordinatewise, find a formula for a unit normal at
P
, or the equivalent written
coordinatewise, find a formula for a unit normal at
P![]() .
.
(b) Does your normal point inwards or outwards? (Either is OK.)
(c) What happens at the poles?
Problem
K-10. (a) Using the method of Problem K-![]() ,
for the Möbius strip described in the handout on
parametric surfaces find a normal vector to the surface for
,
for the Möbius strip described in the handout on
parametric surfaces find a normal vector to the surface for
![]() and again for
and again for
![]() , using the cross
product of partial derivatives.
, using the cross
product of partial derivatives.
(b) Isn't it inconsistent that the two answers are different even though both parameter pairs give the same point on the surface?
Problem
K-11. Using the idea of Problem K-![]() , find a formula
for a perpendicular vector at the
, find a formula
for a perpendicular vector at the ![]() corner of a
Bézier surface patch of degree 2 with control points
corner of a
Bézier surface patch of degree 2 with control points ![]() , where
, where
![]() .
.
Problem K-12. Invent the concept of a quadratic blending of three curves and give an example. (Use Lagrange interpolation.)
Problem
K-13. Describe surfaces that have the form
P![$ (t,u) = \left[\begin{array}{c}t\\ u\\ f( \sqrt{t ^ 2 + u ^ 2})\end{array}\right]$](img189.gif) .
.
Problem
K-14. Consider a Bézier tensor product surface. Explain
how the isoparametric curves are actually Bézier curves in
R![]() . With what control points?
. With what control points?