It is usually best to have the surface be the image of a
rectangle, even if the equations would make sense for all ![]() . Let's say the rectangle is
. Let's say the rectangle is
![]() ,
,
![]() . The choice of
. The choice of ![]() will
depend upon the example.
will
depend upon the example.
A simple approach, the one used by Mathematica, is to imagine
grid lines in the rectangle, compute the grid points where they
cross, compute the images of these points under
P![]() , and
connect them the same way the grid is connected. If your
grid points are dense enough, this gives a good picture,
provided that you have the capability of surface shading,
hidden-line removal, or both.
, and
connect them the same way the grid is connected. If your
grid points are dense enough, this gives a good picture,
provided that you have the capability of surface shading,
hidden-line removal, or both.
If you don't have surface shading or hidden-line removal,
then you have a problem: If you use too many
grid lines, the plot will be too dense and will obscure the
shape of the surface. If you use too few grid lines, your
surface will look jagged instead of smooth, as in Figure
![]() .
.
The solution is a modified method: Use only a few
grid lines, but use more points on each line than just the
grid intersections. Compute the images of all these points
and connect them with line segments the same way they are
connected in the grid. The image of each grid line will
then look like a curve-an isoparametric curve (curve
consisting of points all with one value of ![]() or all
with one value of
or all
with one value of ![]() ), as in Figure
), as in Figure ![]() .
.
Observe the specifications in this example: In the ![]() -direction there are four intervals, each subdivided into
five parts; in the
-direction there are four intervals, each subdivided into
five parts; in the ![]() direction, there are three
intervals, each subdivided into four parts. In a program,
these four numbers (4, 5, 3, 4) should be treated as four
named constants or variables, so that you can easily choose
appropriate values and change them later. The grid
boundaries should also be named constants or variables.
direction, there are three
intervals, each subdivided into four parts. In a program,
these four numbers (4, 5, 3, 4) should be treated as four
named constants or variables, so that you can easily choose
appropriate values and change them later. The grid
boundaries should also be named constants or variables.
To find the actual points used, use this idea: To
subdivide an interval ![]() into
into ![]() pieces, the
subdivision points are
pieces, the
subdivision points are
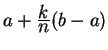 , for
, for
![]() . Notice that you must loop from
. Notice that you must loop from ![]() to
to ![]() ; if you go from
; if you go from ![]() to
to ![]() or
or ![]() to
to ![]() parts of your picture will be missing.
parts of your picture will be missing.
(To invent this formula, imitate the formula for a line
segment:
![]() for
for
![]() describes all numbers in the interval. Now take
describes all numbers in the interval. Now take
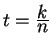 to step across the interval.)
to step across the interval.)
If you are using a language such as PASCAL or C with a program
that plots straight line segments, then to generate the points
and connect them, use two double loops. For the horizontal grid
lines, you'll need an outer loop for ![]() values corresponding
to the heights of the lines and an inner loop for
values corresponding
to the heights of the lines and an inner loop for ![]() values
corresponding to all the points on a horizontal line. For the
vertical grid lines, you'll need another double loop of the same
sort.
values
corresponding to all the points on a horizontal line. For the
vertical grid lines, you'll need another double loop of the same
sort.
For each ![]() point you compute, you can apply
P
point you compute, you can apply
P![]() to it immediately and plot the value; there is no need to
store values computed. (Points where grid lines meet will
be computed twice, but that's OK. By plotting the value is
meant either writing out the value in
E
to it immediately and plot the value; there is no need to
store values computed. (Points where grid lines meet will
be computed twice, but that's OK. By plotting the value is
meant either writing out the value in
E![]() to send
to a plotting program or else doing the projection to two
dimensions yourself and sending the result to a plotting
program.)
to send
to a plotting program or else doing the projection to two
dimensions yourself and sending the result to a plotting
program.)
For some surfaces, the images of the horizontal grid lines will be straight lines. In this case, it often looks better to use just the horizontal grid lines (or just the vertical ones, if their images are straight). In any case, if the image of the grid line on the surface happens to be a straight line, the endpoints of the grid line are already enough; there is no need to use the fine subdivision.
If there is no easy way to remove hidden lines, the plot may look messy if your surfaces have large parts that should be hidden. An easy way to avoid such messiness is to show less of a surface than you could-say, a hemisphere instead of a sphere. For some surfaces, it may be sufficient merely to view them from a good angle.
In Example 2, it can be effective to show not only the surface,
but the original grid as well, drawn in the ![]() -plane. Axes
could also be included.
-plane. Axes
could also be included.
Of course, it isn't necessary to use the grid pattern. Sometimes some other pattern or picture in the parameter domain can be effective.