4. Intersections of lines and line segments

Let's say that a line segment $\overline{AB}$ intersects (or touches) a line $L$ if $\overline{AB}$ and $L$ have at least one point in common, and, more specially, that $\overline{AB}$ crosses $L$ if $A$ and $B$ are not on $L$ but some other point of $\overline{AB}$ is on $L$. Similarly, one line segment could intersect or cross another line segment. Thus, intersecting is a little more general than crossing. In this discussion, let's concentrate on crossing and then see what changes are necessary to handle intersecting. There are different cases, depending on whether we're dealing with lines or line segments and depending on how they are expressed. Two cases are the most important:

Case 1. Does a line segment $\overline{AB}$ cross a line $L$ expressed in the relational form $f(x,y) = 0$, and if so, where?

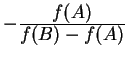This case is the most useful and also the easiest. Method. $\overline{AB}$ crosses $L$ if $f(A)$ and $f(B)$ are nonzero and of opposite signs. To find the crossing point $C$, let $t$ $=$ $- {\frac{\displaystyle f(A)}{\displaystyle f(B) - f(A)}}$ and then let $C$ $=$ $A + t (B-A)$. See Figure .

Figure: A crossing case

Explanation: The key is to observe that if you follow the line segment from $A$ to $B$, the value of $f$ changes at a constant rate. So, for example, if $f(A) = -3$ and $f(B) = 1$, then since $f(C) = 0$, $C$ ought to be ${\frac{3} {4}}$ of the way from $A$ to $B$, i.e., $t$ $=$ ${\frac{3} {4}}$. The ${\frac{3} {4}}$ is the change in value from $A$ to $C$ divided by the change from $A$ to $B$, i.e., $t$ $=$ ${\frac{\displaystyle f(C) -f(A)}{\displaystyle f(B) - f(A)}}$ $=$ ${\frac{\displaystyle 0 - f(A)}{\displaystyle f(B) -f(A)}}$ $=$ $- {\frac{\displaystyle f(A)}{\displaystyle f(B) - f(A)}}$.

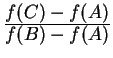
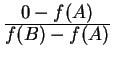
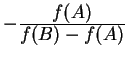Case 2. Do line segments $\overline{AB}$ and $\overline{PQ}$ cross each other, and if so, where?

Method: Use the method of Case 1 both ways around: $\overline{AB}$ should cross the line containing $P$ and $Q$, and vice versa. For each of the two lines, you can use the two-point relational form.

In other words, if the segments are $\overline{PQ}$ and $\overline{AB}$, find all four of $\Delta( P,Q,A)$, $\Delta( P,Q,B)$, $\Delta(A,B,P)$, and $\Delta(A,B,Q)$. The line segments cross each other when all four of these numbers are nonzero, the first two have opposite signs, and the last two have opposite signs. If they do cross each other, the crossing point is $C$ $=$ $A + t (B-A)$, where $t = - {\frac{\displaystyle \Delta(P,Q,A)}{\displaystyle \Delta(P,Q,B) - \Delta(P,Q,A)}}$. See Figure .

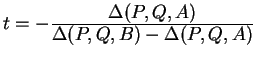Figure: Another crossing case

Note. It is not enough just to check that, say, $\overline{AB}$ crosses the line containing $P$ and $Q$. That can happen even if the two line segments are each an inch long but are a mile from one other. A less extreme example is shown in Figure .

Figure: Another crossing case

What if we are interested in intersecting instead of just crossing, for the case of two line segments $\overline{AB}$, $\overline{PQ}$? The answer is that the circumstances will always be clear from the values of $\Delta( P,Q,A)$, $\Delta( P,Q,B)$, $\Delta(A,B,P)$, and $\Delta(A,B,Q)$, provided not all four of these numbers are zero. For example, if $\Delta(P,Q,A) > 0$, $\Delta(P,Q,B) = 0$, $\Delta(A,B,P)< 0$, $\Delta(A,B,Q) > 0$, then $\overline{AB}$ intersects $\overline{PQ}$ at $B$, somewhere between $P$ and $Q$.

If all four of the $\Delta()$ values are zero, then $A,B,P,Q$ all lie on one line, and a different method is needed: Look at the $x$-coordinates $a _ 1$, $b _ 1$, $p _ 1$, $q _ 1$ or at the $y$-coordinates $a _ 2$, $b _ 2$, $p _ 2$, $q _ 2$ to see the situation. For example, if $a _ 1 < q _ 1 < p _ 1 < b _ 1$, then $\overline{PQ}$ is contained entirely in $\overline{AB}$. (Which should you use, the $x$-coordinates or the $y$-coordinates? A good choice is to use whichever are the more spread out. The ``spread'' of the $x$-coordinates is the maximum of the four $x$-coordinates minus their minimum, and similarly for the ``spread'' of the $y$-coordinates; check which is the greater.)