9. Problems

KK-1. Explain how any line written functionally can be easily rewritten in (a) the usual relational form; (b) in parametric form.

KK-2. Describe how to draw a diagram of $n$ circles, each of radius $r$, whose centers are on a circle of radius $R$ (not drawn) centered at the origin, with connecting line segments as shown. Say explicitly how to find the coordinates of the centers of the circle and of the end points of the line segments. See Figure .

Figure: A diagram with circles

text/CCdir/circ.eps

KK-3. (a) For an affine function $f(x,y) = ax + b y + c$, what is the gradient? (b) For most functions, the gradient depends on the position $(x,y)$. Is this the case for affine functions? (c) What does the graph $z = f(x,y)$ look like?

KK-4. Verify Observation 4 of §3. (Method: What is the relation between the gradient of a function of two variables and the direction of increase?)

KK-5. Verify Observation 3 of §3, using each of these two methods. First method: Consider two points $P = (p _ 1, p _ {2})$ and $Q = (q _ 1, q _ {2})$ on the line and check that $(a,b)$ is perpendicular to $P - Q$. Second method: The gradient of a function of two variables at any point is perpendicular to the level curve of the function through that point. (See the preceding problem.)

KK-6. If the point-normal equation mentioned in Observation 5 of §3 is rewritten as $ax + b y + c = 0$, what is $c$ in terms of    N$$ and $P _ 0$?

KK-7. Explain Observation 6 of §3 by using the point-normal form. (For given    x$$, choose $P _ 0$ to be at the foot of the perpendicular from    x$$.)

KK-8. The relational and parametric representations of a line can each be interpreted in terms of affine functions between spaces. The relational form really expresses the line as the set of points where a certain affine transformation $f:$   R$^ 2 \rightarrow$   R$^ 1$ has value 0 (as mentioned in Observation 6 of §3). The parametric form really expresses the line as the image (set of all values) of an affine transformation    P:   R$^ 1 \rightarrow$   R$^ 2$. In each case, find the extended matrix of the affine transformation involved.

KK-9. Suppose you want to rotate a line $30 ^\circ$ counterclockwise about the origin. (a) If the line is given in relational form, how can you describe the new coefficients $a', b', c'$ in terms of the old $a,b,c$? (b) If the line is given parametrically, how can you describe the new $P _ 0$ and    v$$ in terms of the old $P _ 0$ and    v$$? (Leave the answers in terms of products of matrices and vectors, without multiplying out.) (c) If the line is given in functional form $y = mx + b$, express the functional form of the rotated line in terms of $m$ and $b$.

KK-10. Given two points $P$, $Q$, suppose we started from the equation $\Delta (P,Q,$x$) = 0$. In §4 it is explained how we could be sure the equation has the form $ax + b y + c = 0$. (a) In this equation, how could we be sure that not both $a$ and $b$ are zero, so that it does represent some line $L$? (An equation $0x + 0y + 0 = 0$ would represent the whole plane; an equation $0x + 0y + c = 0$ with $c \neq 0$ would represent the empty set.) (b) From the definition of $\Delta (P,Q,$x$)$, why is it obvious that both $P$ and $Q$ are on $L$?

KK-11. Show that the circle in    R$^ 2$ through three noncollinear points $A = (a _ 1, a _ {2})$, $B = (b _ 1, b _ {2})$, and $C = (c _ 1, c _ {2})$ is given by

$\det \left[\begin{array}{cccc} a _ 1 ^ 2 + a _ 2 ^ 2& a _ 1& a _ 2& 1\\ b _ 1... ... + c _ 2 ^ 2& c _ 1& c _ 2& 1\\ x ^ 2 + y ^ 2& x& y& 1 \end{array}\right] = 0$.

Use these three steps: (a) Show that all three points satisfy the equation. (b) By expanding the determinant in a suitable way, show that the equation has the form $E x ^ 2 + E y ^ 2 + Fx + Gy + H = 0$, where $E \neq 0$. (c) Explain why the graph of any equation of this form is a circle or a single point or the empty set. (By (a), though, the graph is not a single point or empty, so it's a circle.)

KK-12. (a) (A high-school problem) Inscribe a triangle in a semicircle of radius 1 so that one side of the triangle is the diameter of the circle. What choice of the third vertex of the triangle minimizes the area outside the triangle? (b) (The relevance for us) Given a fixed base $\overline{PQ}$ for a triangle and specified area $A$, describe the set of all points $R$ for which the triangle $PQR$ has area $A$, and say what this answer has to do with $\Delta (P,Q,R)$.

KK-13. (a) If you are looking at two points $P$ and $Q$ from a point $R$ and $\Delta (P,Q,R) > 0$, is $Q$ to the right or to the left of $P$, as seen from $R$? (b) In    R$^ 2$, is $Q$ to the right or to the left of $P$ as seen from $R$, where $P = (2,3)$, $Q=(3,4)$, $R = (8,6)$?

KK-14. Show that if $P,Q,R$ are three points in    R$^ 2$, then $\Delta (P,Q,R)$ equals the third component of the cross product in    R$^ 3$ of $(P-R,0)$ and $(Q-R,0)$. (Use properties of determinants.)

KK-15. For points in    R$^ 3$, suppose we write $\Delta(P,Q,R,$x$)$ $=$ $ax + b y + cz + d$. The corresponding normal vector to the plane through $P$, $Q$, and $R$ is $(a,b,c)$. To see if this normal vector is slanted up (so that the ``positive half-space'' is the half-space above the plane rather than below), we need to check that $c > 0$. The problem: Show that $c$ $=$ $- \Delta(\overline P, \overline Q, \overline R)$, where $\overline P$, $\overline Q$, $\overline R$ are orthographic projections on the $x,y$-plane. (Method: Expansion by cofactors.)

KK-16. Show that it is not possible to have exactly three of the four numbers $\Delta( P,Q,A)$, $\Delta( P,Q,B)$, $\Delta(A,B,P)$, $\Delta(A,B,Q)$ be zero.

KK-17. (a) Consider the three line segments $\overline{AB}$, $\overline{CD}$, $\overline{EF}$, where $A = (4,1)$, $B = (1,6)$, $C = (4,4)$, $D = (3,2)$, $E = (3,5)$, $F = (2,4)$. Find explicitly the corresponding affine functions from the two-point form. (Give coefficients numerically.) (b) Using (a) determine which pairs among these line segments cross. (There are three possible pairs to consider.) (c) Find the points at which the pairs you listed in (b) cross.

KK-18. In Case 2 of §5, list as many different ways as possible for how the four numbers $\Delta( P,Q,A)$, $\Delta( P,Q,B)$, $\Delta(A,B,P)$, $\Delta(A,B,Q)$ could be negative, zero, or positive. Make a sketch to illustrate each way. To eliminate some cases that are similar to others, assume that $\Delta( P,Q,A)$ $\leq$ $\Delta( P,Q,B)$, that $\Delta(A,B,P)$ $\leq$ $\Delta(A,B,Q)$, that $\Delta( P,Q,A)$ $\leq$ $\Delta(A,B,P)$, and that not all four numbers are zero.

KK-19. Explain explicitly step-by-step how a computer could determine whether the line segments $\overline{AB}$ and $\overline{PQ}$ intersect, where $A = (-10,0)$, $B = (30,2)$, $P = (50,3)$, $Q = (10,1)$.

KK-20. Is the point $P = (6,5)$ inside the non-convex polygon with vertices $A = (7,5.5)$, $B = (9,4)$, $C = (7,8)$, $D = (5,4.5)$, $E = (3,6)$, $F = (5,2)$ (in order)?

Do this problem twice, by using Method #1 and then Method #2 of §8. (For this particular polygon and choice of $P$, all angles should come out to be multiples of $\frac 14 \pi$.)

KK-21. If line segments $\overline{AB} , \overline{CD}$ in    R$^ 3$ are viewed from above at infinity , does one appear to pass above the other, and if so, which, where $A = (1,2,0)$, $B = (4,-1,3)$, $C = (4,1,1)$, and $D = (3,-1,2)$? Use a method suitable for a computer.

(Suggested: First determine whether the projections of $\overline{AB} , \overline{CD}$ on the $x,y$-plane cross. If they do, then use the same $t,u$ for the original segments to find the two points that appear to the viewer to be on top of one another. See which of the two points has the greater $z$-value.)

KK-22. Consider any line $L$ in    R$^ 2$. Designate the half-plane on one side as ``positive'' and the other half-plane as ``negative''. The corresponding signed distance function $D(x,y)$ is simply the perpendicular distance of $(x,y)$ from $L$ if $(x,y)$ is in the positive half-plane, or minus that distance if $(x,y)$ is in the negative half-plane. The signed distance function ought to be an affine function defining $L$. Is it? (To see, start with any affine function defining $L$ and scale it, using Observation 6 of §3.)

KK-23. Proposition. The distance of the point $(x,y)$ from the line with equation $ax + b y + c = 0$ is the absolute value of ${\frac{\displaystyle ax + b y + c}{\displaystyle \sqrt {a ^ 2 + b ^ {2}}}}$.

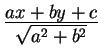Prove this proposition by using Observation 6 of §3. (The fraction is an affine function. What is the length of its normal?)

KK-24. In    R$^ 2$, consider the triangle $PQR$, with $P = (8,1)$, $Q = (3,6)$, $R = (13,11)$. Find the barycentric coordinates of these points: $Q$ itself, $A = (8,6)$, $B = (5,4)$, $C = (9,7.5)$.

KK-25. Sketch a triangle $PQR$ in the plane. (a) Indicate on it the point with barycentric coordinates $( {\frac{1} {2}}, 0, {\frac{1} {2}}) _ {bary}$ and the point with $(0, {\frac{1} {2}}, {\frac{1} {2}}) _ {bary}$. (b) Indicate all points with $c _ 3 = {\frac{1} {2}}$. (c) Indicate all points with $c _ 3 = .25$ and all points with $c _ 3 = .75$.

KK-26. Show that barycentric coordinates in a triangle are invariant under translation, and in fact are invariant under any affine transformation. (Method: Starting from a relation $S = c _ 1 P + c _ 2 Q + c _ 3 R$ with $c _ 1 + c _ 2 + c _ 3 = 1$, apply an affine transformation $T($x$) =$   x$A +$   b$$ and see if the same relation holds between the image points $P',Q',R',S'$, where $P' = T(P)$ and so on.)

KK-27. Prove Proposition 3 of §9. (Method: Given $S$, write $S-R$ as a linear combination of the linearly independent vectors $P-R$ and $Q-R$.)

KK-28. Prove Proposition 5 of §9. (Take the vector equation $c _ 1 P + c _ 2 Q + c _ 3 R = S$ and write it as two equations, one for each coordinate. Then with the equation $c _ 1 + c _ 2 + c _ 3 = 1$, you have three equations in three unknowns. Use Cramer's rule to solve them, and show that you get the result wanted. Use the fact that $\det A = \det A ^ t$.)

KK-29. Take a triangle $PQR$ such that $\Delta (P,Q,R) > 0$. For each point in the plane, each of the three barycentric coordinates could be $<0$, $=0$, or $> 0$, making $3 \cdot 3 \cdot 3 = 27$ conceivable outcomes. Break the plane into regions (some of which could be single points or pieces of lines) based on outcomes that actually occur. How many regions are there (twenty-seven, or some smaller number)? Make a sketch with labels for each of your regions.

KK-30. Invent barycentric coordinates for a tetrahedron in    R$^ 3$ and state facts similar to those in §9.

KK-31. Describe in detail an algorithm to draw the pattern shown in Figure . Here $P = (1,1)$, $Q = (5,3)$, $R = (3,6)$.

Figure: A pattern of telescoping triangles

KK-32. Describe in detail an algorithm to draw the pattern shown in Figure . Assume that you have a plotting package that will draw a circle if you tell it the center and the radius.

Figure: A pattern with circles

text/CCdir/bowling.eps

KK-32. Is the point $(6,8)$ inside the triangle with vertices $(6,7)$, $(3,4)$, $(7,10)$? Use a method suitable for a computer.