Proposition 3. Let ![]() be three noncollinear
points in
R
be three noncollinear
points in
R![]() . Then every point
. Then every point ![]() in the
plane can be written uniquely in the form
in the
plane can be written uniquely in the form ![]()
![]()
![]() , where
, where
![]()
![]()
![]() .
.
Definition. In the Proposition,
![]() are called the barycentric coordinates of
are called the barycentric coordinates of ![]() with
respect to
with
respect to ![]() . Let's write
. Let's write
![]() for the barycentric coordinates of a point.
for the barycentric coordinates of a point.
For example, the center of mass ![]() of the
triangle
of the
triangle ![]() is the obtained by averaging the three
vertices, so has barycentric coordinates
is the obtained by averaging the three
vertices, so has barycentric coordinates
![]() . In fact,
``barycentric'' means ``weight-centered''. As another example,
. In fact,
``barycentric'' means ``weight-centered''. As another example,
![]() itself has barycentric coordinates
itself has barycentric coordinates
![]() . See Figure
. See Figure ![]() .
.
Barycentric coordinates are often handy when you need to do something with a triangle that treats all three vertices the same way. The points inside the triangle are easily identified:
Proposition 4. A point ![]() is inside the triangle
is inside the triangle ![]() (or on an edge) if and only if its three barycentric
coordinates with respect to
(or on an edge) if and only if its three barycentric
coordinates with respect to ![]() are all nonnegative.
are all nonnegative.
Recall that a convex combination is a linear
combination in which the coefficients are nonnegative and
have sum ![]() . Thus the points inside the triangle are
the convex combinations of
. Thus the points inside the triangle are
the convex combinations of ![]() ,
, ![]() , and
, and ![]() .
.
Proposition 5. The barycentric coordinates of the point
x![]() with respect to
with respect to ![]() ,
, ![]() , and
, and ![]() have
the values
have
the values
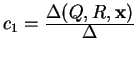 ,
,
 ,
,
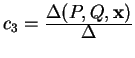 ,
,
where ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Thus ![]() (for example) is obtained by
scaling the two-point relational form for the line through
(for example) is obtained by
scaling the two-point relational form for the line through
![]() and
and ![]() , so is an affine function of position
itself. We could write
, so is an affine function of position
itself. We could write
![]() x
x![]() . The scale
factor of
. The scale
factor of
![]() is just what is needed to
have
is just what is needed to
have ![]()
![]()
![]() , as it should be. In
particular,
, as it should be. In
particular, ![]() is zero on the line through
is zero on the line through ![]() and
and ![]() , and is constant on each line parallel to that
line.
, and is constant on each line parallel to that
line.