4. Interpolation by relaxed cubic splines

Suppose that you are interested not in controlled design but in interpolation. In other words, data points $S_0,\dots, S_n$ are given and you want a relaxed cubic spline curve $P(t)$ for $0 \leq t \leq n$ such that $P(i) = S_i$; i.e., the curve goes through the data points.

One easy approach is to use B-splines as an intermediate step. This time, though, you know the points $S_0,\dots, S_n$ and you must compute the appropriate control points $B_0,\dots, B_n$ before you will be able to compute the Bézier control points for the individual pieces.

Of course, $B_0 = S_0$ and $B_n = S_n$. To find $B_1,\dots, B_{n-1}$, we can use the linear equations already found above for the $S_i$ in terms of the $B_i$ and solve them treating the $B_i$ as unknowns and the $S_i$ as constants. When the linear equations are written in matrix form, they look like this (for $n = 5$):

$\left[\begin{array}{cccc}4&1&0&0\\ 1&4&1&0\\ 0&1&4&1\\ 0&0&1&4\end{array}\right]$ $\left[\begin{array}{c}B _ 1\\ B _ 2\\ B _ 3\\ B _ 4\end{array}\right]$ $=$ $\left[\begin{array}{c}(6 S _ 1 - S _ 0)\\ 6 S _ 2\\ 6 S _ 3\\ (6 S _ 4 -S _ 5) \end{array}\right]$

Here the $B_i$ and $S_i$ are points, so that in    R$^2$ they are pairs of numbers. These equations are equivalent to two sets of equations with the same coefficient matrix, one set for $x$ coordinates and one for $y$ coordinates. To solve them, though, it is easiest to use one of two more direct methods. Let $M$ be the matrix of coefficients (which we can call the ``1 4 1 matrix''), let $B_*$ be the matrix whose rows are $B_1,\dots B_{n-1}$, and let $C$ be the matrix of constants on the right.

Method 1

(on a computer): Make the augmented matrix $[M \vert C]$ and row-reduce it completely. The answer will be $[I \vert B_*]$.

Method 2

(on homework problems or tests): You will be given $M^{-1}$; the solution is then $B_* = M^{-1} C$.

Note: The $(n-1) \times (n-1)$ matrix $M$ is nonsingular for any $n$. In general, a matrix is guaranteed to be well behaved if its diagonal entries are all large in absolute value compared to the sums of the absolute values of the off-diagonal entries in each row.

Problem. Find Bézier control points for the four segments of the relaxed cubic spline curve through the data points $S_0 = (1,-1)$, $S_1 = (-1,2)$, $S_2 = (1,4)$, $S_3 = (4,3)$, $S_4 = (7,5)$, as shown in Figure . Useful information:

${ {\left[\begin{array}{ccc}4&1&0\\ 1&4&1\\ 0&1&4\end{array}\right]}}^{-1} = ... ...}}} {\left[\begin{array}{rrr}15&-4&1\\ -4&16&-4\\ 1&-4&15\end{array}\right]}$.

Figure: Data points for interpolation

Solution. $n=4$, so the ``1 4 1'' equations in matrix form are $3 \times 3$:

${\left[\begin{array}{ccc}4&1&0\\ 1&4&1\\ 0&1&4\end{array}\right]} \left[\begin{array}{c} B _ 1\\ B _ 2\\ B _ 3\end{array}\right]$ $=$ $\left[\begin{array}{c}(6 S _ 1 - S _ 0)\\ 6 S _ 2\\ (6 S _ 3 - S _ 4)\end{array}\right]$ $=$ $\left[\begin{array}{rr}-7&13\\ 6&24\\ 17&13\end{array}\right]$. Solving these equations by using the matrix inverse, we get

$\left[\begin{array}{c}B _ 1\\ B _ 2\\ B _ 3\end{array}\right]$ $=$ ${{\frac{\displaystyle 1}{\displaystyle 56}}} {\left[\begin{array}{rrr}15&-4&1\\ -4&16&-4\\ 1&-4&15\end{array}\right] }$ ${\left[\begin{array}{rr}-7&13\\ 6&24\\ 17&13\end{array}\right]}$ $=$ ${\left[\begin{array}{rr}-2&2\\ 1&5\\ 4&2\end{array}\right]}$

Therefore the B-spline control points are $B_0 = S_0 = (1,-1)$, $B_1 = (-2,2)$, $B_2 = (1,5)$, $B_3 = (4,2)$, $B_4 = S_4 = (7,5)$. The four sets of cubic Bézier control points are as follows, and together they give Bézier curves that go together to make the curve shown in Figure .

$$\begin{array}{lcccc} \mbox{B\'ezier \char93 1:}& (1,-1)& (0,... ...\'ezier \char93 4:}& (4,3)& (5,3)& (6,4)& (7,5)\\ \end{array}$$

Figure: The interpolating relaxed B-spline curve

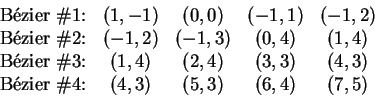
Derivation of the ``1 4 1'' equations. The first and last equations are different from the middle ones. For all equations, recall that ${\frac 1 6} B_{i-1} + {\frac 2 3} B_i + {\frac 1 6} B_{i+1} = S_i$. For the middle equations, just multiply this relation by $6$ to get

$1 \cdot B_{i-1} + 4 \cdot B_i + 1 \cdot B_{i+1} = 6 \cdot S_i$.

For the first equation, $B_0 + 4 B_1 + B_2 = 6 S_1$; recall that $B_0 = S_0$ and subtract $S_0$ from both sides. The last equation is handled similarly, by using the fact that $B_n = S_n$.

Remark. As you see, we used B-splines to do interpolation. Usually when you hear someone talk about a ``B-spline'' problem, though, the control points $B_i$ will be given; when you hear someone talk about a ``spline interpolation'' problem, the $S_i$ will be given and the person may or may not be thinking of using B-splines to get the answer.