


Next: b_vectors
Up: b_vectors
Previous: b_vectors
4. The projection of a vector on a line
Suppose a vector
v is projected onto a line.
Figure:
A vector projected onto a line
|

|
The direction of the line can be expressed two
ways: By giving a unit vector
u along the line, or
by giving an arbitrary nonzero vector
w along the line,
in which case we can take
u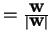 .
.
- (11)
- The length of the projection of
v on the line is
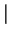 v
v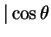
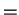 v
v u, where a negative sign
means that the projection has direction opposite to
u. The
length can also be expressed as
u, where a negative sign
means that the projection has direction opposite to
u. The
length can also be expressed as
 .
.
- (12)
- The vector projection of
v on the line
is therefore
 v
v u
u u (scalar times vector).
This vector projection can be called the vector
component of
v in the direction of the line.
u (scalar times vector).
This vector projection can be called the vector
component of
v in the direction of the line.
- (13)
- If the direction of the line is expressed
with an arbitrary nonzero vector
w, the vector
projection of
v on the line becomes
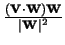 or
or
 .
.
- (14)
- The vector component of
v perpendicular
to the line is just
v minus the vector component along
the line, so it is equal to
v
 v
v u
u u or
v
u or
v .
.
- (15)
- A plane is described using a normal
N or unit normal
n. The vector component of
v
perpendicular to the plane is
 v
v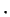 n
n n or
n or
 and the vector component of
v
along the plane (i.e., the projection of
v on the plane)
is
v
and the vector component of
v
along the plane (i.e., the projection of
v on the plane)
is
v v
v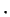 n
n n or
v
n or
v . These sound the other way around from
(
. These sound the other way around from
(![[*]](/lib/latex2html-icons/crossref.gif) ) and (
) and (![[*]](/lib/latex2html-icons/crossref.gif) ) because
N is
already perpendicular to the plane.
) because
N is
already perpendicular to the plane.



Next: b_vectors
Up: b_vectors
Previous: b_vectors
Kirby A. Baker
2002-01-04

![]() .
.