


Next: b_vectors
Up: b_vectors
Previous: b_vectors
3. The dot product
The dot product or scalar product or inner
product of vectors
v and
w (say in
R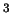 ) is
) is
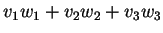 , denoted
v
, denoted
v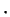 w.
In geometrical terms,
v
w.
In geometrical terms,
v w
w v
v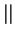 w
w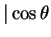 , where
, where 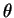 is the angle between
v and
w. The dot product makes sense in
R
is the angle between
v and
w. The dot product makes sense in
R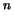 for any
for any
 .
.
The dot product has many uses:
- (1)
-
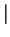 v
v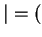 v
v v
v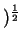 .
.
- (2)
-
v
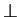 w precisely when
v
w precisely when
v w
w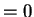 . (The zero vector
0 is considered to be
perpendicular to all vectors.)
. (The zero vector
0 is considered to be
perpendicular to all vectors.)
- (3)
- The angle
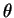 between two nonzero
vectors
v and
w in
R
between two nonzero
vectors
v and
w in
R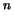 satisfies
satisfies
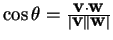 . Notice, though,
that
. Notice, though,
that
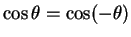 , so the sign of
, so the sign of 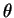 is not determined by the dot product, even in
R
is not determined by the dot product, even in
R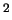 ,
where it is natural to say a counterclockwise angle is
positive and a clockwise angle is negative.
,
where it is natural to say a counterclockwise angle is
positive and a clockwise angle is negative.
- (4)
- By (
![[*]](/lib/latex2html-icons/crossref.gif) ), if
v
), if
v w
w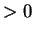 then the
angle between the vectors is between
then the
angle between the vectors is between 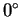 and
and  in absolute value; if
v
in absolute value; if
v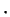 w
w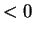 , the
angle is between
, the
angle is between  and
and
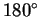 in absolute
value.
in absolute
value.
- (5)
-
i
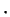 v
v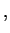 j
j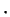 v
v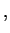 k
k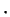 v are
the components of
v, so
v
v are
the components of
v, so
v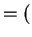 i
i v
v j
j v
v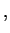 k
k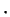 v
v .
.
- (6)
- The dot product of two unit vectors is
simply the cosine of the angle between them.
- (7)
- By (
![[*]](/lib/latex2html-icons/crossref.gif) ) and (
) and (![[*]](/lib/latex2html-icons/crossref.gif) )
together, you can see that the components of a unit vector
u are the cosines of the angles that
u makes with
i
)
together, you can see that the components of a unit vector
u are the cosines of the angles that
u makes with
i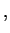 j
j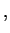 k, or in other words, the cosines of the angles that
u makes with the
k, or in other words, the cosines of the angles that
u makes with the 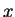 -,
-, 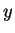 -, and
-, and 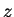 -axes. For this
reason the components of a unit vector are called direction
cosines.
-axes. For this
reason the components of a unit vector are called direction
cosines.
- (8)
- In a matrix product
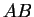 , each entry of
, each entry of
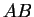 is the dot product of a row of
is the dot product of a row of 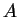 with a column of
with a column of
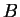 .
.
- (9)
- Let
v,
w be vectors in
R
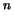 ,
written as row vectors. Then
w
,
written as row vectors. Then
w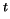 is a column vector.
The matrix product
v w
is a column vector.
The matrix product
v w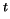 makes sense and its value is
a
makes sense and its value is
a
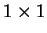 matrix, which is the same thing as a scalar.
By (
matrix, which is the same thing as a scalar.
By (![[*]](/lib/latex2html-icons/crossref.gif) ), this scalar is just
v
), this scalar is just
v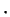 w. To
summarize:
v
w. To
summarize:
v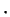 w
w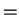 v w
v w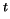 .
.
- (10)
- In
R
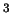 , the equation of the plane through
the point
, the equation of the plane through
the point
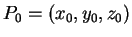 with normal
N
with normal
N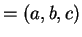 is
N
is
N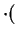 x
x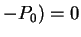 , or equivalently,
, or equivalently,
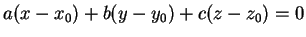 , or
equivalently,
, or
equivalently,
 , where
, where
 N
N P
P .
.
Similarly, in
R , the equation of the line
through the point
, the equation of the line
through the point
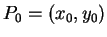 perpendicular to
the vector
N
perpendicular to
the vector
N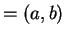 is
is
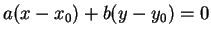 . However, usually we deal with lines parametrically, as in
§
. However, usually we deal with lines parametrically, as in
§![[*]](/lib/latex2html-icons/crossref.gif) .
.
Note: For clarity, in this course let's try to
use
n when we mean a unit normal and
N when we
mean a normal of any nonzero length.



Next: b_vectors
Up: b_vectors
Previous: b_vectors
Kirby A. Baker
2002-01-04
![]() ) is
) is
![]() , denoted
v
, denoted
v![]() w.
In geometrical terms,
v
w.
In geometrical terms,
v![]() w
w![]() v
v![]() w
w![]() , where
, where ![]() is the angle between
v and
w. The dot product makes sense in
R
is the angle between
v and
w. The dot product makes sense in
R![]() for any
for any
![]() .
.
![]() , or
equivalently,
, or
equivalently,
![]() , where
, where
![]() N
N![]() P
P![]() .
.
![]() , the equation of the line
through the point
, the equation of the line
through the point
![]() perpendicular to
the vector
N
perpendicular to
the vector
N![]() is
is
![]() . However, usually we deal with lines parametrically, as in
§
. However, usually we deal with lines parametrically, as in
§![]() .
.