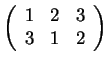2.1. Cycles

A permutation is a cycle if some symbols go in a single cycle when the permutation is repeated, while the other symbols stay fixed.

Example: 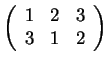$\left(\begin{array}{ccc}1&2&3\ 3&1&2\end{array}\right)$ is a cycle since we have $1 \mapsto 3 \mapsto 2 \mapsto 1$.

For short such a cycle is written $\left(\begin{array}{ccc}1&3&2\end{array}\right)$, again meaning $1 \mapsto 3 \mapsto 2 \mapsto 1$.

On five symbols, one cycle is $\left(\begin{array}{cccc}1&4&2&5\end{array}\right)$, meaning $1 \mapsto 4 \mapsto 2 \mapsto 5 \mapsto 1$ and $3 \mapsto 3$. A cycle of length $k$ is called a $k$-cycle. A 2-cycle is called a transposition.

Proposition. Any permutation on $n$ symbols can be written as a product of disjoint (non-overlapping) cycles. For example, one permutation in $S_4$ is $(13)(24)$.

Since disjoint cycles commute, the order doesn't make a difference.

Problem V-12. Do $(12)$ and $(23)$ commute?

Problem V-13. Write 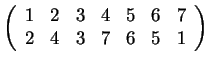$\left(\begin{array}{ccccccc}1&2&3&4&5&6&7\\ 2&4&3&7&6&5&1\end{array}\right)$ as a product of disjoint cycles. (Omit 1-cycles.)

Problem V-14. Write out the multiplication table of $S_3$ using cycle notation. The elements are $\mathbf{1}$ (meaning the identity transformation), 3-cycles, and 2-cycles (transpositions).