2.0. Definitions

Definition. A permutation of a set $X$ is a one-to-one correspondence on $X\rightarrow X$.

Sometimes we are interested in permutations of a specific set, such as rows of a matrix, as in Problem V-. It is important, though, to understand the structure of various permutations on $n$ symbols for each specific value of $n$, and for that it makes little difference what the set is. Therefore we often use $X = \{1,2,\dots, n\}$ as a set of symbols to permute.

The set of permutations on $\{1,\dots, n\}$ is denoted $S_n$, the symmetric group on $n$ symbols¹. For example, there are six permutations on three symbols, so $S_3$ has six elements. In general, $S_n$ has $n!$ elements.

Temporarily, let's describe permutations by writing the symbols each with its image beneath. For example,

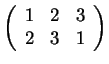$\left(\begin{array}{ccc}1&2&3\ 2&3&1\end{array}\right)$ means the permutation for which $1 \mapsto 2, 2 \mapsto 3, 3 \mapsto 1$.

Definition. Permutations are multiplied by taking their composition.

Problem V-11. What is $\left(\begin{array}{ccc}1&2&3\ 2&3&1\end{array}\right) \left(\begin{array}{ccc}1&2&3\ 2&1&3\end{array}\right)$?

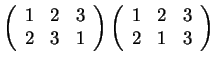(Method: We are composing functions $f$ and $g$. Find $f(g(1)), f(g(2)), f(g(3))$ and then write the answer in the matrix-like form².)