1. Details

The Bézier curve is just a particular linear combination of the control points with time-varying coefficients. If the control points are $P_0$, $P_1$, $P_2$, $P_3$, then the curve is given by

$P(t) = (1-t)^3 P_0 + 3 (1-t)^2 t P_1 + 3 (1-t) t^2 P_2 + t^3 P_3$, for $0 \leq t \leq 1$.

Why these coefficients? They arise in a way related to binomial expansions. Recall that $(s+t)^3$ $=$ $s^3 + 3 s^2 t + 3 s t^2 + t^3$. Now consider these terms individually rather than added together, and put $(1-t)$ for $s$. You get four functions of $t$, called the Bernstein polynomials¹. These are

$$\begin{array}{ccccc} J_{3,0} (t)&=&(1-t)^3&=&1 (1-t)^3 t^0\\ ... ...(1-t)^1 t^2\\ J_{3,3} (t)&=& t^3&=&1 (1-t)^0 t^3 \end{array}$$

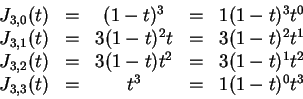
Thus for a Bézier curve,

$P(t) = J_{3,0} (t) P_0 + J_{3,1} (t) P_1 + J_{3,2} (t) P_2 + J_{3,3} (t) P_3$.

As you will see, the Bernstein polynomials have nice properties that are reflected in the properties of Bézier curves. Bernstein polynomials and Bézier curves can be defined for any degree $n$ by using the expansion of $(s+t)^n$, but let's continue to concentrate on the case of degree $3$, since that case is most frequently used.

Figure: Example

Example. Suppose the control polygon has
$P _ 0 = (2,3)$, $P _ 1 = (0,5)$, $P _ 2 = (-1,-2)$, and $P _ 3 = (2,1)$, as in Figure . Then
$P(t) = J_{3,0} (t) P_0 + J_{3,1} (t) P_1 + J_{3,2} (t) P_2 + J_{3,3} (t) P_3$
$=$ $(1-t) ^ 3 (2,3) + 3(1-t) ^ 2 t (0,5) + 3(1-t)t ^ 2 (-1,-2) + t ^ 3 (2,1)$
$=$ $(2 - 6 t + 3 t^2 + 3 t^3, 3 + 6 t - 27 t^2 + 19 t^3)$

In other words, $P(t) = (x(t),y(t))$ with $x(t) = 2 - 6 t + 3 t^2 + 3 t^3$ and
$y(t) = 3 + 6 t - 27 t^2 + 19 t^3$.