next up previous
Next: x_lagrange Up: x_lagrange Previous: x_lagrange

6. Newton's approach to interpolation

There is also an approach due to Newton for solving polynomial interpolation problems by using ``divided differences''. The method will be explained here for the case $ n=3$, without proof, but it works the same for every $ n $.

Suppose, then, that times $ t _ 0,\dots, t _ 3$ are given along with data points $ P _ 0,\dots, P _ 3$. As usual, we want a polynomial curve of degree at most $ 3$ with $ P(t _ i) = P _ i$ for each $ i $.

Step 1. Compute quantities

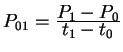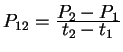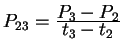$ P _ {01} = {\frac{\displaystyle P _ 1 - P _ 0}{\displaystyle t _ 1 - t _ 0}}$, $ P _ {12} = {\frac{\displaystyle P _ 2 - P _ 1}{\displaystyle t _ 2 - t _ 1}}$, $ P _ {23} = {\frac{\displaystyle P _ 3 - P _ 2}{\displaystyle t _ 3 - t _ 2}}$.



Step 2. Compute quantities

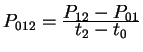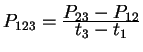$ P _ {012} = {\frac{\displaystyle P _ {12} - P _ {01}}{\displaystyle t _ 2 - t _ 0}}$, $ P _ {123} = {\frac{\displaystyle P _ {23} - P _ {12}}{\displaystyle t _ 3 - t _ 1}}$.



Step 3. Compute the quantity

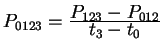$ P _ {0123} = {\frac{\displaystyle P _ {123} - P _ {012}}{\displaystyle t _ 3 - t _ 0}}$.



Step 4.
Let $ P(t) = P _ 0 + (t-t _ 0) P _ {01} + (t-t _ 0)(t - t _ 1) P _ {012} + (t-t _ 0)(t - t _ 1)(t - t _ 2) P _ {0123}$.

(For general $ n $ there would be steps 1 through $ n+1 $.)

The quantities $ P _ {i\dots j}$ are called divided differences. They can be thought of as making a triangular table, as shown. A column of $ t $-values has been added for convenience. The boxes indicate the entries actually used in the last step. (The other entries aren't wasted, as they have been used in computing the boxed entries.)

$ t $ $ P_i $ $ P _ {i,i+1}$ $ P _ {i,i+1,i+2}$ $ P _ {i,i+1,i+2,i+3}$
$ t_0 $ \fbox{\(P _ 0\)}      
    \fbox{\(P _ {01}\)}    
$ t _ 1$ $ P _ 1$   \fbox{\(P _ {012}\)}  
    $ P _ {12}$   \fbox{\(P _ {0123}\)}
$ t _ 2$ $ P _ 2$   $ P _ {123}$  
    $ P _ {23}$    
$ t _ 3$ $ P _ 3$      

As you see, each entry $ P _ {i,\dots, j}$ with more than one subscript is obtained as a quotient, where the numerator is the difference of the entries immediately to the left ( $ P _ {i+1,\dots, j} - P _ {i,\dots, j-1}$), and the denominator is the difference of the $ t $-values for the outer subscripts ( $ t _ j - t _ i$).

This method is often easier to do by hand than the blending-function method, and it is also easier to program, but it is less helpful in understanding other computer graphics methods for curves.



Example: The second curve in Figure [*] has data points $ (0,0)$, $ (1,0)$, $ (1,1)$, and $ (2,1)$. The table of divided differences is as follows. (The denominators of $ {\frac 1 2}$ come from $ 2-0$ and $ 3-1$ and the $ \frac 13$ comes from $ 3-0$.)

$ t $ $ P_i $ $ P _ {i,i+1}$ $ P _ {i,i+1,i+2}$ $ P _ {i,i+1,i+2,i+3}$
0 \fbox{\((0,0)\)}      
    \fbox{\((1,0)\)}    
$ 1 $ $ (1,0)$   \fbox{\((-{\frac 1 2},{\frac 1 2})\)}  
    $ (0,1)$   \fbox{\((\frac 13,-\frac 13)\)}
$ 2$ $ (1,1)$   $ ({\frac 1 2},-{\frac 1 2})$  
    $ (1,0)$    
$ 3$ $ (2,1)$      

Thus the curve is $ P(t) = (0,0) + t(1,0) + t(t-1)(-{\frac 1 2},{\frac 1 2}) + t(t-1)(t-2)(\frac 13, -\frac 13)$.

next up previous
Next: x_lagrange Up: x_lagrange Previous: x_lagrange
Kirby A. Baker 2002-02-13