Problem
FF-1. Consider the bilinear patch
![]() with corner data
with corner data
![]() ,
,
![]() . Describe the
horizontal cross-section (level curve) for
. Describe the
horizontal cross-section (level curve) for ![]() , and the vertical
cross-section for the plane given by
, and the vertical
cross-section for the plane given by ![]() .
.
Problem
FF-2. For the bilinear patch
P![]() with corner data
with corner data ![]() ,
,
![]() ,
, ![]() ,
, ![]() , find a formula for
P
, find a formula for
P![]() .
.
Problem
FF-3. For a linearly blended Coons surface
![]() consider
these corner heights and boundary curves:
consider
these corner heights and boundary curves:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() . (a) Is this data consistent?
(b) If it is, find an equation for the surface. (The answer may
be left as a product of matrices.)
. (a) Is this data consistent?
(b) If it is, find an equation for the surface. (The answer may
be left as a product of matrices.)
Problem FF-4. Explain in detail why the formula for constructing a parametric interpolating spline surface does give the desired interpolation.
Problem
FF-5. (a) If ![]() is the nonparametric relaxed bicubic
spline surface with
is the nonparametric relaxed bicubic
spline surface with ![]() and with value 0 at
and with value 0 at ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() and
and
![]() , find
, find ![]() .
(You may use any earlier problems that deal with the case
.
(You may use any earlier problems that deal with the case ![]() ,
,
![]() .)
.)
(b) If ![]() is the parametric relaxed bicubic spline surace
with
is the parametric relaxed bicubic spline surace
with ![]() and
and
![]() for
for ![]() among
among
![]() , find
, find ![]() . (Here
. (Here ![]() is from part (a). If you
handle each coordinate separately it should not be necessary to
consider many basis functions.)
is from part (a). If you
handle each coordinate separately it should not be necessary to
consider many basis functions.)
Problem FF-6. A piecewise bicubic spline surface (as made with a tensor basis of uniform relaxed interpolating splines) can be thought of as one patch over a rectangle, or it can be regarded as made up of many smaller patches glued together, with each one having a unit square as a domain. What kind of function is being used on each unit square?
Problem
FF-7. (a) Explain why a Lagrange surface that has degree 1 in
both ![]() and
and ![]() and has
and has
![]() and
and
![]() is an instance of a bilinear patch (Example 10).
(b) What about a relaxed cubic spline surface, still with
is an instance of a bilinear patch (Example 10).
(b) What about a relaxed cubic spline surface, still with ![]() on both coordinates?
on both coordinates?
Problem
FF-8. Here are control points for a Bézier surface with tensor-product
basis, for ![]() . Describe what the surface should look like, either in
words or by an intuitive sketch.
The ``middle four'' control points are the corners of a square in the
. Describe what the surface should look like, either in
words or by an intuitive sketch.
The ``middle four'' control points are the corners of a square in the ![]() plane; specifically,
plane; specifically,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . All the other control points
are at the origin.
. All the other control points
are at the origin.
Problem
FF-9. Consider the parametric Bézier surface ![]() with
with ![]() and control points
and control points ![]() given by
given by
![]() except that
except that
![]() . Since
. Since ![]() , you will need the Bernstein polynomials
, you will need the Bernstein polynomials
![]() ,
,
![]() ,
,
![]() .
.
(a) Find the coordinate functions of ![]() . (Use tensor basis;
simplify algebraically.)
. (Use tensor basis;
simplify algebraically.)
(b) Sketch ![]() . (Just sketch the six isoparametric curves
for
. (Just sketch the six isoparametric curves
for ![]() and
and ![]() values
values ![]() .)
.)
Problem
FF-10. Write down an expression for a Lagrange surface with
![]() for the data points
for the data points
![]() , with
, with ![]() ,
, ![]() , for
, for ![]() and
and ![]() ,
except that
,
except that
![]() . Then simplify the expression.
(Method: Simplify one coordinate at a time. It can help to use any
properties you know about linear combinations of Lagrange basis functions.
Of course, if you can guess a function that fits the data, then by
the uniqueness of the Lagrange solution that must be correct, so
the algebra is avoided.)
. Then simplify the expression.
(Method: Simplify one coordinate at a time. It can help to use any
properties you know about linear combinations of Lagrange basis functions.
Of course, if you can guess a function that fits the data, then by
the uniqueness of the Lagrange solution that must be correct, so
the algebra is avoided.)
Problem
FF-11. Recall that a partial derivative with respect to one
variable is just the derivative when all other variables are held
fixed. For a parametric surface
P![]() , observe that the
two partial derivatives
, observe that the
two partial derivatives
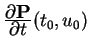 and
and
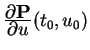 give velocity vectors of the two isoparametric curves at
P
give velocity vectors of the two isoparametric curves at
P![]() . These two vectors are therefore tangent to
the surface, and their cross product is a normal (a
perpendicular) to the surface.
. These two vectors are therefore tangent to
the surface, and their cross product is a normal (a
perpendicular) to the surface.
(a) For the sphere parameterized as
P![]() , or the equivalent written
coordinatewise, find a formula for a unit normal at
P
, or the equivalent written
coordinatewise, find a formula for a unit normal at
P![]() .
.
(b) Does your normal point inwards or outwards? (Either is OK.)
(c) What happens at the poles?
Problem
FF-12. (a) Using the method of Problem FF-![]() ,
for the Möbius strip described in the handout on
parametric surfaces find a normal vector to the surface for
,
for the Möbius strip described in the handout on
parametric surfaces find a normal vector to the surface for
![]() and again for
and again for
![]() , using the cross
product of partial derivatives.
, using the cross
product of partial derivatives.
(b) Isn't it inconsistent that the two answers are different even though both parameter pairs give the same point on the surface?
Problem
FF-13. Using the idea of Problem FF-![]() , find a formula
for a perpendicular vector at the
, find a formula
for a perpendicular vector at the ![]() corner of a
Bézier surface patch of degree 2 with control points
corner of a
Bézier surface patch of degree 2 with control points ![]() , where
, where
![]() .
.
Problem FF-14. Invent the concept of a quadratic blending of three curves and give an example. (Use Lagrange interpolation.)
Problem
FF-15. Describe surfaces that have the form
P![]() .
.
Problem
FF-16. Consider a Bézier tensor product surface. Explain
how the isoparametric curves are actually Bézier curves in
R![]() . With what control points?
. With what control points?
Problem
FF-17. Suppose you want to interpolate a nonparametric
relaxed uniform cubic spline surface
![]() with
with ![]() for data values
for data values
![]() and
and
![]() otherwise, where
otherwise, where ![]() ,
, ![]() . Find
. Find
![]() .
(Use a tensor basis. The answer is simpler than you might anticipate.)
.
(Use a tensor basis. The answer is simpler than you might anticipate.)