4. Tensor bases

For curves, you have studied interpolation (using the Lagrange method or splines) and controlled design (Bézier or B-splines). It is possible to use analogous methods for surfaces. The key is to find a good way of making basis functions; the rest is easy.

Let's concentrate on the case of interpolating splines and look first at the nonparametric case. To ease the later transition to the parametric case, let's look at $z$ as a function of $t$ and $u$ rather than of $x$ and $y$.

Suppose, then, that we are considering functions $z(t,u)$ with $0 \leq t \leq 4$ and $0 \leq u \leq 4$, and that at integer grid points we have given heights to interpolate, say $z _ {ij}$ at $t=i,u=j$.

Step 1. Construct basis functions $f _ 0(t),\dots, f _ 4(t)$ for relaxed uniform interpolating cubic splines. Thus $f _ i (j) = \left \{ \begin{array}{l}1 \mbox{ if }i=j\\ 0 \mbox{ if }i \neq j \end{array}\right .$.

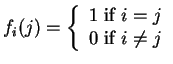From these make basis functions in two variables by simply taking $f _ i (t) f _ j (u)$ for $i = 0,\dots, 4$ and $j = 0,\dots, 4$. The graph of $f _ 2(t)f _ 3(u)$ is shown in Figure . Notice that this function has value 1 only at one grid point, namely at $(2,3)$, and it has value 0 at all other grid points--a nice property. These basis functions are said to form a tensor basis, a term that refers to a basis made of products.

Figure: One tensor-basis function in two variables

Step 2. Let $z(t,u) = \sum _ {ij} z _ {ij} f _ i (t) f _ j (u)$. Then the graph is a surface that does interpolate at grid points as desired, i.e., $z(i,j) = z _ {ij}$. (Why?)

Observe that since the $f _ i (t)$ are piecewise cubic, the tensor-basis functions and the final result $z(t,u)$ are piecewise bicubic (cubic in each variable when the other variable is held fixed).

Basis functions for several types of curves are shown in Figure , all for the case $n=4$.

Figure: Bases for n=4

Now let's do a parametric version, where we need to interpolate given data points $P _ {ij}$, and let's suppose that the parameter domain is $0 \leq t \leq m$, $0 \leq u \leq n$. Since $m$ and $n$ might not be the same, the first step is to construct basis functions separately for each parameter: $f _ 0(t),\dots, f _ m (t)$ and $g _ 0 (u),\dots, g _ n (u)$. Then the tensor basis functions are $f _ i (t)g _ j (u)$, and the interpolating surface is given by

P$(t,u) = \sum _ {ij} f _ i (t) g _ j (u) P _ {ij}$.

A compact way to write this is to make a matrix of the points:

P$(t,u) = \left[\begin{array}{ccc}f _ 0(t),\dots, f _ m(t)\end{array}\right]\lef... ...y}\right]\left[\begin{array}{c}g _ 0(u)\\ \dots \\ g _ n(u)\end{array}\right]$.

Applying the same idea in other contexts gives Lagrange interpolation for surface, and Bézier surfaces and B-spline surfaces for controlled design. In each case you can find one-parameter basis functions (Bernstein polynomials in the case of Bézier curves), and then use them to make a tensor basis. The control points make a control polyhedron, although (just as for a control polygon) it is not a solid object but rather consists of polygons with control points as vertices.