next up previous
Next: About this document ... Up: o_fields Previous: o_fields

2. Problems1

Problem O-1. For the field $ \mathbb{F}_ 8$, it is a fact that there is a generator $ \alpha$ that is a root of the irreducible polynomial $ x^3 + x + 1$, so $ \alpha^3 = 1 + \alpha$. Also, since $ \alpha$ is a generator of the seven nonzero elements, we know $ \alpha ^ 7 = 1$.

(a) Make a table showing how to write each power of $ \alpha$ as a linear combination of the basis $ 1, \alpha, \alpha^2$. In the table, use blank spaces to indicate 0 coefficients. The table will start

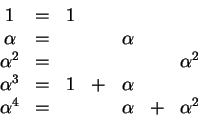
\begin{displaymath}\begin{array}{ccccccc} 1 & = & 1 \\ \alpha & = & & & \alpha... ...\ \alpha ^ 4 & = & & & \alpha & + & \alpha^2 \\ \end{array}\end{displaymath}

From there on, multiply through by $ \alpha$ and simplify using what we know about $ \alpha^3$.

It is handy to use the powers of $ \alpha$ when multiplying and the linear combinations when adding.

(b) Find $ (1 + \alpha + \alpha^2)^2$ as a linear combination of $ 1, \alpha, \alpha^2$ by using the table.

(c) Find $ \alpha^3 + \alpha^4$ as a power of $ \alpha$ by using the table.



Problem O-2. (a) For $ a \neq 0 $ in $ \mathbb{F}_ {p^k}$, show that $ a^{p^k -1} = 1$.

(Method: Like Fermat and Euler.)

(b) Show that $ a^{p^k} = a$ for any $ a$ in $ \mathbb{F}_ {p^k}$.

(Method: Start with (a) and multiply through by $ a$.)

(c) Let $ \phi:\mathbb{F}_ {p^k}\rightarrow \mathbb{F}_ {p^k}$ be given by $ \phi(a) = a^p$. Show that $ \phi^k(a)$, meaning $ \phi(\phi(\dots (\phi(a))\dots ))$ $ k$ times, equals $ a$ for every $ a$ in the field.



Problem O-3. Show that in a finite field $ F$ of characteristic $ p$, the map $ \phi: F\rightarrow F$ given by $ \phi(a) = a^p$ is an automorphism--an isomorphism of the field with itself. You will need to show

(i) $ \phi(ab) = \phi(a) \phi(b)$

(ii) $ \phi(a+b) = \phi(a) + \phi(b)$. (What do you know about binomial coefficients?)

(iii) $ \phi$ is one-to-one from $ F$ onto $ F$.

(Method for (iii): You may quote (c) of the preceding problem, whether or not the problem was assigned. If $ \phi$ is not one-to-one, could a composition of $ \phi$ with itself be one-to-one? Similary for onto?)



Problem O-4. (a) Show that if a unit $ a$ in $ \mathbb{Z}/m\mathbb{Z}$ has order $ r$ and $ r'\vert r$ then $ a^{r/r'}$ has order $ r'$.

(b) Show that if $ r$ and $ s$ are positive integers and $ \ell =$   lcm$ (r,s)$ then there are divisors $ r'$ and $ s'$ of $ r$ and $ s$ respectively such that $ \ell = r's'$ and $ r'$ and $ s'$ are coprime.

(Method: Use prime factorizations.)

(c) Prove (g)-(ii) on p. H 2: If a commutative ring $ R$ has a unit $ a$ of order $ r$ and a unit $ b$ of order $ s$, then $ R$ has a unit of order $ \ell$ where2 $ \ell =$   lcm$ (r,s)$. (Note that this element is not necessarily $ ab$, since for example if $ b = a^{-1}$ then $ a$ and $ b$ have the same order $ r$ and lcm$ (r,r) = r$, but $ ab = 1$, which is an element of order 1.)

(Method: Use (a) and (b) and N-3.)

(d) Show that in $ \mathbb{Z}/m\mathbb{Z}$ if the maximum order of a unit is $ r$ then the order of every unit actually divides $ r$.

Then by (a), the possible orders of units are $ r$ and all its divisors.

(Method: If $ a$ has the maximum possible order, $ r$, and another unit $ b$ has order $ s$, what about lcm$ (r,s)$?)



Problem O-5. Prove that a finite field has a generator for the nonzero elements.

(Method: You may quote (d) of the preceding problem, whether or not it was assigned. If the maximum order of an element is $ r$, show that $ a^r = 1$ for every nonzero element $ a$. In that case, every nonzero element is a root of $ x^r - 1$. You know how to compare the number of roots and the order. So how large must $ r$ be? And remember, there is an element of order $ r$.)

next up previous
Next: About this document ... Up: o_fields Previous: o_fields
Kirby A. Baker 2004-06-07