-
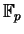 is contained in
is contained in 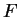 as a subfield;
as a subfield;
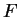 is a vector space over
is a vector space over
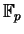 ;
;
- if the vector-space dimension of
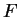 over
over
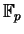 is
is 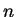 ,
then
,
then 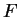 has
has 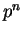 elements.
elements.
- there is a finite field of size
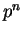 ;
;
- there is only one field of size
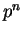 , ``up to isomorphism''.
(This means that any two fields of that size must be isomorphic.)
, ``up to isomorphism''.
(This means that any two fields of that size must be isomorphic.)
- Our name for this field is
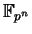 . (Some books
call the field
GF
. (Some books
call the field
GF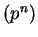 for ``Galois field''.)
for ``Galois field''.)
- We have discussed the specific examples
-
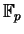 (
(
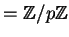 ) for each prime
) for each prime 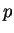 .
.
-
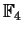
-
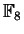
-
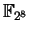 (in connection with Rijndael)
(in connection with Rijndael)
-
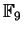
-
- The powers of
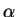 are all the nonzero elements;
are all the nonzero elements;
- the order of
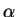 is
is 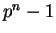 , if the field
has
, if the field
has 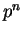 elements;
elements;
-
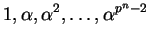 are all the nonzero
elements. (Why
are all the nonzero
elements. (Why 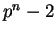 and not
and not 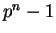 ?)
?)
The next power ![]() can be re-expressed as a linear combination of
lower powers using the irreducible polynomial.
can be re-expressed as a linear combination of
lower powers using the irreducible polynomial.