1. Problems

Problem H-1. Explain: The order of $a$ is also the number of distinct elements (including 1) that are powers of $a$.

Problem H-2. (i) Which of the statements in §1 are true in any finite ring with 1? (ii) Which statements are true in any finite field?

Problem H-3. (i) Show that $a^p \equiv a$ in $\mathbb{Z}_ p$, whether or not $p\vert a$.

(ii) More generally, invent and prove a similar statement for a power of $a$ in $\mathbb{Z}_ m$, involving $\phi(m)$.

Problem H-4. If the units of $\mathbb{Z}_ m$ have a generator, show that there are $\phi(\phi(m))$ units in all.

Problem H-5. Show that in the field $\mathbb{Z}_ p$ (for a prime $p$), if $a$ is any nonzero element then $a^{\frac {p-1}2} = \pm 1$.

(Method: Let $b = a^{\frac{p-1}2}$ and observe that $b^2 = 1$. Solve for $b$ as in high-school algebra.)

Problem H-6. (i) Show that for positive integers $d$ and $n$, if $d \vert n$ and $d \neq n$, then $d \vert {\frac{\displaystyle n}{\displaystyle q}}$ for some prime divisor $q$ of $n$. (Suggestion: Think in terms of the prime factorization of $n$.)

Example²: $4\vert 60$ so $4 \vert$ (at least) one of ${\frac{\displaystyle 60}{\displaystyle 2}}$, ${\frac{\displaystyle 60}{\displaystyle 3}}$, ${\frac{\displaystyle 60}{\displaystyle 5}}$, of which the last two work.

(ii) Apply this idea to show that an element $a$ in $\mathbb{Z}_ p$ is not a generator of the units if and only if $a^{(p-1)/q} = 1$ for some prime factor $q$ of $p-1$.

In other words, if the powers of $a$ return to 1 too soon, then one of the places they return to 1 is a power of the form given.

This provides a quick test for whether an element is a generator!

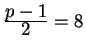Example: In $\mathbb{Z}_ {17}$, the only prime factor of $p-1 = 16$ is 2 and ${\frac{\displaystyle p-1}{\displaystyle 2}} = 8$, so an element $a$ is not a generator if and only if $a^8 = 1$. Testing 2: $2^4 = -1$ so $2^8 = 1$, not a generator. Testing 3: $3^4 = 81 = -4$ and $3^8 = 16 = -1$, so $3$ is a generator. In fact, in $\mathbb{Z}_ {17}$ all nonzero elements will have 8th power equal to $\pm 1$, by Problem H-; therefore the generators are the elements, such as 3, whose 8th power is $-1$.

(iii) Use the calculators on the course home page to find a generator for (a) $\mathbb{Z}_ {31}$; (b) $\mathbb{Z}_ {151}$ (which you can see is prime by using the factoring routine). Say what you did.

Note: The calculators will accept simple expressions such as 150/3 in place of an explicit integer.

Problem H-7. Let $p$ be the first prime past 10 million. Find the smallest generator of the units of $\mathbb{Z}_ p$.

(Use the calculators on the home page for testing primality, for factoring $p-1$, and for residues of powers. Be careful about the numbers of zeros in integers! Include a record of the calculations you tried.)

Problem H-8. Use the Chinese Remainder Theorem to explain why the powers of $2$ in $\mathbb{Z}_ {24}$ cycle the way they do.

Problem H-9. Prove (d)-(iii) in §1.

Problem H-10. Prove (g)-(i) in §1.