next up previous
Next: About this document ... Up: e_hw4 Previous: e_hw4

Assignment #4

Due Friday, April 30.



Read ยง6D on your own. We'll do more with this later.



To do but not hand in:

p. 84, Ex. 1;

p. 86, Ex. 3;

p. 90, Ex. 8;

E-1, E-5 below.



To hand in:

p. 84, Ex. 3;

p. 86, Ex. 4;

pp. 89-90, Ex's 4 and 9;

D-2 (which previously was ``not to hand in'');

E-2, E-3, and E-4 below.



Problem E-1. Find the remainder when $ 3^{10110 _ 2}$ is divided (a) by 16; (b) by 17. Check using the power routine on the course home page.



Problem E-2. Some primes are sums of two squares, e.g., $ 13 = 2^2 + 3^2$.

(a) Show using congruences that such a prime is either 2 or is of the form $ 4n + 1$ for some $ n$.

(b) An interesting fact is that every prime of the form $ 4n + 1$ is the sum of two squares, and in only one way (up to ordering). Write each of 29, 61, and 97 as the sum of two squares.



Problem E-3. Recall the proof that $ \sqrt 2 $ is irrational. There is a much more general fact that is no harder to prove.

A real number is called an algebraic integer if it is the root of a polynomial with integer coefficients and leading coefficient 1: $ x^n + c _ {n-1} x^{n-1} + \dots + c _ 1 x + c _ 0$.

Examples: $ \sqrt 2 $ is an algebraic integer since it is a root of the polynomial $ x^2 - 2$. Also, 7 is an algebraic integer since it's the root of $ x - 7$.

Notice that the concept of an algebraic integer is more general than the concept of an ordinary integer, not more special. Also, the definition of algebraic integer can be used for complex numbers too, but we won't.



Theorem. A (real) algebraic integer is either an ordinary integer or irrational.

(a) Explain why this theorem shows $ \sqrt 2 $ is irrational (and $ \sqrt 3, \sqrt 5, \sqrt 6$, etc., too).

(b) Prove the theorem.

Suggested method: Suppose that a fraction $ {\frac{\displaystyle a}{\displaystyle b}}$ in lowest terms (so $ a,b$ are coprime and $ b > 0$) is a root of $ x^n + c _ {n-1} x^{n-1} + \dots + c _ 1 x + c _ 0$, i.e., that

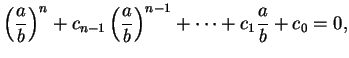
$\displaystyle \left (\frac ab \right )^n + c _ {n-1} \left (\frac ab \right )^{n-1} + \dots + c _ 1 \frac ab + c _ 0 = 0,$

where $ c _ {n-1},\dots, c _ 0$ are integers, and try to show that $ b = 1$, so that $ \frac ab$ must be an integer. To do so, multiply through to clear the denominator, write $ a^n = \dots $, factor out whatever you can on the right-hand side, and try to reason that if $ b$ were not 1 then $ b$ would have a prime factor that causes a difficulty leading to a contradiction.

(c) Prove that $ \sqrt{\sqrt 5 + 1} $ is irrational.



Problem E-4. To make very large primes, one way is to look for primes of the form $ b^n - 1$, where $ b$ and $ n$ are integers. But most values of $ b$ and $ n$ won't work.

(a) Explain why, if $ b^n - 1$ is prime with $ n > 1$, then $ b$ must be 2.

(Useful: Recall from algebra that $ b^n -1 = (b - 1)(1 + b + b^2 + \dots + b^{n-1})$; this arises in summing a finite geometric series. Or if that isn't familiar, just expand the right-hand side to check.)

(b) Explain why, if $ 2^n - 1$ is prime, then $ n$ itself must be prime. (Suggestion: If $ n$ factors nontrivially, turn that into a violation of (a).)

(c) Let's write $ M _ p = 2^p - 1$, where $ p$ is prime. If $ M _ p$ is prime, it is called a Mersenne prime. The catch is that $ M _ p$ might not be prime, depending on the prime $ p$. Find the lowest prime $ p$ for which $ M _ p$ is not prime. (To test numbers for being prime, you may use the factoring program on the class home page.)

Note: People search for large Mersenne primes to test advanced factoring programs. In fact, at the moment the largest known prime is a Mersenne prime. For the latest record, see http://www.mersenne.org/prime.htm .



Problem E-5. Continuing from Problem Problem E-[*]: Another way to make large primes is to look for primes of the form $ b^n + 1$.

(a) Show that if $ b^n + 1$ is prime with $ n > 1$, then $ b$ must be even. (Easy.)

(b) Show that if $ b^n + 1$ is prime with $ n > 1$, then $ n$ must be even.

(Useful: Putting $ -b$ for $ b$ in the earlier problem, observe that if $ n$ is odd then $ b^n + 1 = (b + 1)(1 - b + b^2 - \dots + b^{n-1})$. For example, $ x^3 + 1$ factors as $ (x + 1)(1 - x + x^2)$.)

(c) Show that in fact, if $ b^n + 1$ is prime with $ n > 1$, then $ n$ cannot have any odd factors at all. In other words, $ n$ must be a power of 2.

(d) Consider the case $ b = 2$ and write $ F _ k = 2^{2^k} + 1$, for $ k = 1, 2, 3, \dots $. $ F _ k$ might or might not be prime, depending on $ k$, but if it is prime then it is called a Fermat prime. Find the first $ k$ for which $ F _ k$ is not prime, using the factorization routine on the class home page and perhaps a hand calculator. (Possibly useful: the calculator will accept an input expression involving + and/or *, but unfortunately not one involving exponentiation.)

next up previous
Next: About this document ... Up: e_hw4 Previous: e_hw4
Kirby A. Baker 2004-04-24