For Problem EE-1:
The statement to be proved is that for any square matrix ![]() ,
any
,
any ![]() eigenvectors corresponding to distinct eigenvalues are
linearly independent.
eigenvectors corresponding to distinct eigenvalues are
linearly independent.
For ![]() the statement is trivially true, since an eigenvector
is nonzero.
the statement is trivially true, since an eigenvector
is nonzero.
Now consider the case of any ![]() , assuming the statement holds
for the case
, assuming the statement holds
for the case ![]() . Suppose the eigenvectors are
. Suppose the eigenvectors are
![]() , corresponding to eigenvalues
, corresponding to eigenvalues
![]() . Suppose
. Suppose
Therefore the statement is true for all ![]() (really all
(really all ![]() ,
where
,
where ![]() is
is
![]() ), by induction.
), by induction.
For Problem EE-2:
In the case ![]() , the first
, the first ![]() and the last
and the last ![]() don't
overlap in the middle. (It's clear that this is the first case
to examine, since we know it's really false for
don't
overlap in the middle. (It's clear that this is the first case
to examine, since we know it's really false for ![]() .)
.)
For Problem EE-3:
(a) We know that multiplying ![]() on the left by
on the left by ![]() scales
the rows of
scales
the rows of ![]() and multiplying on the right by
and multiplying on the right by ![]() scales
the columns of
scales
the columns of ![]() . An off-diagonal entry will get
incompatible scalings. In particular,
. An off-diagonal entry will get
incompatible scalings. In particular,
![]() and
and
![]() ,
so if
,
so if ![]() then
then
![]() .
If
.
If ![]() then since the diagonal entries of
then since the diagonal entries of ![]() are distinct,
we get
are distinct,
we get
![]() .
.
(b) As suggested, the map
![]() preserves
multiplication, so if we choose
preserves
multiplication, so if we choose ![]() to diagonalize
to diagonalize ![]() to
to ![]() and we let
and we let
![]() , then
, then ![]() . The diagonal
entries of
. The diagonal
entries of ![]() are the eigenvalues of
are the eigenvalues of ![]() and so are distinct.
Then by (a),
and so are distinct.
Then by (a), ![]() is diagonal and we have diagonalized
is diagonal and we have diagonalized ![]() .
Since the same
.
Since the same ![]() was used for both
was used for both ![]() and
and ![]() , they are
simultaneously diagonalizable.
, they are
simultaneously diagonalizable.
For Problem EE-4:
Following the suggestion, if ![]() then applying the map
then applying the map
![]() we get
we get ![]() . Now
. Now ![]() commutes
with
commutes
with ![]() , which is
, which is ![]() , so by Problem EE-
, so by Problem EE-![]() (a),
(a),
![]() is diagonal. Since
is diagonal. Since
![$ E ^ 2 = \left[\begin{array}{rr}9&0\\ 0&1\end{array}\right]$](img45.gif) , we must
have
, we must
have
![$ E = \left[\begin{array}{rr}\pm 3& 0\\ 0& \pm 1\end{array}\right]$](img46.gif) . Then there are only four
possibilities for
. Then there are only four
possibilities for
![]() .
.
For Problem EE-5:
(Many of the problems I made up for class examples and homework
are like this. I usually start with an easy ![]() of
determinant 1 such as
of
determinant 1 such as
![$ P = \left[\begin{array}{rr}3&1\\ 2&1\end{array}\right]$](img48.gif) ).
).
For Problem EE-6:
For convenience let
![$ R = R _ {90 ^ \circ} =
\left[\begin{array}{rr}0&-1\\ 1&0\end{array}\right]$](img49.gif) . We have
. We have
![]() . The roots are
. The roots are
![]() . For
. For
![]() we get
we get
![$ P - iI = \left[\begin{array}{rr}-i&-1\\ 1&-i\end{array}\right]$](img53.gif) . Although this might
not instantly look singular, it has to be! An eigenvector is
obtained by solving
. Although this might
not instantly look singular, it has to be! An eigenvector is
obtained by solving
![]() ; choosing
; choosing ![]() we get
we get
![]() , so the eigenvector is
, so the eigenvector is
![$ \left[\begin{array}{r}1\\ -i\end{array}\right]$](img57.gif) . For
. For
![]() , everything works the same with
, everything works the same with ![]() in place of
in place of ![]() ,
so an eigenvector is
,
so an eigenvector is
![$ \left[\begin{array}{r}1\\ i\end{array}\right]$](img61.gif) . Therefore
. Therefore
![]() with
with
![$ D = \left[\begin{array}{rr}i&0\\ 0&-i\end{array}\right]$](img63.gif) and
and
![$ P = \left[\begin{array}{rr}1&1\\ -i&i\end{array}\right]$](img64.gif) .
.
For Problem EE-7:
![]() . (Remember,
. (Remember, ![]() here!) Neither 0 nor 1 is a root, so
here!) Neither 0 nor 1 is a root, so ![]() is not
diagonalizable over GF(2). Now look in GF(4). Not
surprisingly,
is not
diagonalizable over GF(2). Now look in GF(4). Not
surprisingly, ![]() and
and ![]() turn out to be roots
(using the operation tables), so these are the eigenvalues. They
are distinct, so
turn out to be roots
(using the operation tables), so these are the eigenvalues. They
are distinct, so ![]() is diagonalizable.
is diagonalizable.
If we were asked actually to diagonalize ![]() , we could do it:
For
, we could do it:
For
![]() ,
,
![$ A - \alpha I = \left[\begin{array}{cc}(1-\alpha)&1\\ 1&-\alpha\end{array}\right]
= \left[\begin{array}{rr}\beta&1\\ 1&\alpha\end{array}\right]$](img70.gif) . This matrix has to be singular,
and in fact the second row is
. This matrix has to be singular,
and in fact the second row is ![]() times the first row.
Solve
times the first row.
Solve
![]() by taking
by taking ![]() ,
, ![]() .
Similary, if we take
.
Similary, if we take
![]() the roles of
the roles of ![]() and
and ![]() are reversed. Thus we get
are reversed. Thus we get
![]() with
with
![$ P = \left[\begin{array}{rr}1&1\\ \beta&\alpha\end{array}\right]$](img75.gif) and
and
![$ D = \left[\begin{array}{rr}\alpha&0\\ 0&\beta\end{array}\right]$](img76.gif) .
.
For Problem EE-8:
If the eigenvalues are distinct, the blocks are all
![]() ,
which means the Jordan form is diagonal!
,
which means the Jordan form is diagonal!
For Problem EE-9:
Put ![]() in Jordan form by
in Jordan form by
![]() . Since
. Since ![]() ,
applying the similarity map we get
,
applying the similarity map we get ![]() . In squaring
. In squaring ![]() ,
each Jordan block gets squared. For a block
,
each Jordan block gets squared. For a block ![]() , we
have
, we
have
![]() . (Example:
. (Example:
![$ \left[\begin{array}{rrr}r&0&0\\ 1&r&0\\ 0&1&r\end{array}\right] ^ 2 = \left[\begin{array}{rrr}r^2&0&0\\ 2r&r^2&0\\ 1&2r&r^2\end{array}\right]$](img84.gif) .)
If
.)
If ![]() we can see that
we can see that ![]() has an entry of 1 where
has an entry of 1 where
![]() has an entry of 0, so
has an entry of 0, so
![]() . But even for
. But even for ![]() ,
matching entries, we get
,
matching entries, we get ![]() , so
, so ![]() or
or ![]() .
On the other hand, unless the block is
.
On the other hand, unless the block is
![]() , we have
, we have
![]() , which gives
, which gives ![]() , an impossibility. Therefore
all the Jordan blocks are
, an impossibility. Therefore
all the Jordan blocks are
![]() and
and ![]() is diagonalizable.
is diagonalizable.
For Problem EE-10:
By Cayley's theorem we just need a matrix with
![]() . One such matrix is
. One such matrix is
![$ A = \left[\begin{array}{rr}1&1\\ 1&0\end{array}\right]$](img94.gif) .
.
For Problem EE-11:
Apply ![]() to the sphere, where
to the sphere, where
![$ D = \left[\begin{array}{rrr}a&0&0\\ 0&b&0\\ 0&0&c\end{array}\right]$](img96.gif) .
The sphere is turned into the desired ellipsoid and the volume is
changed by a factor of
.
The sphere is turned into the desired ellipsoid and the volume is
changed by a factor of
![]() . Therefore the formula
is
. Therefore the formula
is
![]() .
.
For Problem EE-12:
In the definition of the determinant using permutations, there is
only one nonzero term, which corresponds to the permutation used
to make the matrix from ![]() . Therefore the determinant equals
the sign of the permutation.
. Therefore the determinant equals
the sign of the permutation.
For Problem EE-13:
The permutation definition has ![]() terms each with 9 multiplications,
so we get
terms each with 9 multiplications,
so we get
![]() . On the other hand, by
elementary row operations we need
. On the other hand, by
elementary row operations we need
![]() , if we count division as multiplication by an inverse.
, if we count division as multiplication by an inverse.
For Problem EE-14:
The answer is that you need to look inside just one container.
Now that you know a lot about ![]() , you should think this
way: Each arrangement of the tops is a permutation. For
example
, you should think this
way: Each arrangement of the tops is a permutation. For
example
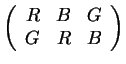 means that the container with
the red marble has a top marked G, etc. There are six
permutations in
means that the container with
the red marble has a top marked G, etc. There are six
permutations in ![]() : the identity, two 3-cycles, and three
transpositions (2-cycles). The identity and the transpositions
have at least one top correct, which is excluded by the problem.
Therefore you need to distinguish between just two possibilities.
The 3-cycles (R B G) and (R G B) can be recognized by knowing
where just one letter goes, so you need to look in only one
container.
: the identity, two 3-cycles, and three
transpositions (2-cycles). The identity and the transpositions
have at least one top correct, which is excluded by the problem.
Therefore you need to distinguish between just two possibilities.
The 3-cycles (R B G) and (R G B) can be recognized by knowing
where just one letter goes, so you need to look in only one
container.
Example: If the container with a red marble has the top marked G, the permutation must be (R G B), so the container with the green marble is marked B and the container with the blue marble is marked R.
For Problem EE-15:
The only possibilities are the identity map, transpositions,
3-cycles, 4-cycles, and the product of two disjoint transpositions:
![]() . We saw in an earlier problem that
an
. We saw in an earlier problem that
an ![]() -cycle is the product of
-cycle is the product of ![]() transpositions, so
transpositions are odd, 3-cycles are even, and 4-cycles are odd,
and of course
transpositions, so
transpositions are odd, 3-cycles are even, and 4-cycles are odd,
and of course
![]() is even.
is even.
Incidentally, a useful vocabulary word is ``parity'', meaning
``evenness or oddness''. So we can say an ![]() -cycle has the
opposite parity from
-cycle has the
opposite parity from ![]() itself.
itself.
For Problem EE-16:
(a) The new basis vector ![]() is written in terms of the old
basis as
is written in terms of the old
basis as
![]() , so its coordinate vector is
, so its coordinate vector is
![$ \left[\begin{array}{r}1\\ 1\\ 1\end{array}\right]$](img110.gif) , and similarly
for
, and similarly
for ![]() and
and ![]() . So the change-of-basis matrix is
. So the change-of-basis matrix is
![$ P = \left[\begin{array}{rrr}1&1&1\\ 1&1&2\\ 1&-2&1\end{array}\right]$](img113.gif) .
.
(b) We need to solve for ![]() ,
, ![]() ,
, ![]() in
terms of
in
terms of
![]() . The answer is the inverse of
the matrix from (a):
. The answer is the inverse of
the matrix from (a):
![$ \left[\begin{array}{rrrrrr}1&1&1&1&0&0\\ 1&1&2&0&1&0\\ 1&-2&1&0&0&1\end{arra...
...53&-1&\frac 13\\
0&1&0&\frac 13&0&-\frac 13\\ 0&0&1&-1&1&0\end{array}\right]$](img118.gif) , so the change-of-basis matrix
is
, so the change-of-basis matrix
is
![$ \left[\begin{array}{rrr}\frac 53&-1&\frac 13\\ \frac 13&0&-\frac 13\\ -1&1&0\end{array}\right]$](img119.gif) .
.
(c) Solve for new basis elements in terms of old:
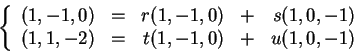
By inspection the first equation gives
![]() .
The second equation gives
.
The second equation gives
![]() , so
, so
![]() .
The change-of-basis matrix is
.
The change-of-basis matrix is
![$ P = \left[\begin{array}{rr}r&t\\ s&u\end{array}\right] = \left[\begin{array}{rr}1&-1\\ 0&2\end{array}\right]$](img124.gif) .
.
(d) As usual, the coordinate vector of ![]() with respect to the standard
basis is
with respect to the standard
basis is ![]() itself. Therefore the change-of-basis matrix is
itself. Therefore the change-of-basis matrix is
![]() .
.
(e) Write the new basis with respect to the old:
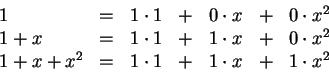
So the change-of-basis matrix is
![$ P = \left[\begin{array}{rrr}1&1&1\\ 0&1&1\\ 1&1&1\end{array}\right]$](img128.gif) .
.
For Problem EE-17:
(a) The determinant is
![]() .
.
(b) The matrix is invertible because its determinant is a product of nonzero terms and so is nonzero.
(c) We get equations
![]()
![]()
![]()
which is the same as
![]() c
c![]() b for
b for
![$ A = \left[\begin{array}{rrr}1&2&4\\ 1&3&9\\ 1&5&25\end{array}\right]$](img134.gif) ,
c
,
c![$ = \left[\begin{array}{r}c _ 0\\ c _ 1\\ c _ 2\end{array}\right]$](img135.gif) ,
b
,
b![$ = \left[\begin{array}{r}8\\ 7\\ 1\end{array}\right]$](img136.gif) .
.
Since ![]() is a van der Monde matrix with distinct
is a van der Monde matrix with distinct
![]() ,
,
![]() is nonsingular. Therefore there is a unique solution.
is nonsingular. Therefore there is a unique solution.
(d) As suggested, taking a linear relation and applying powers of ![]() ,
we get equations
,
we get equations
 .
.
Let
![]() . Then these equations are
. Then these equations are
![$ P \left[\begin{array}{r}r _ 1\\ {\dots }\\ r _ k\end{array}\right] =$](img139.gif) 0,
0,
![$ P \left[\begin{array}{r}r _ 1 \lambda _ 1 \\ {\dots }\\ r _ k \lambda _ k\end{array}\right] =$](img140.gif) 0,
0,
![$ P \left[\begin{array}{r}r _ 1 \lambda _ 1 ^ 2 \\ {\dots }\\ r _ k \lambda _ k ^ 2 \end{array}\right] =$](img141.gif) 0,
...,
0,
...,
![$ P \left[\begin{array}{r}r _ 1 \lambda _ 1 ^ {k-1}\\ {\dots }\\ r _ k \lambda _ k ^ {k-1}\end{array}\right] =$](img142.gif) 0. Putting these together,
0. Putting these together,
![$ P \left[\begin{array}{ccccc}
r _ 1&r _ 1 \lambda _ 1&r _ 1 \lambda _ 1 ^ 2&{\d...
...mbda _ k ^ 2&{\dots }&
r _ k \lambda _ k ^ {k-1}\end{array}\right] = \mathcal O$](img143.gif) , or
, or
![$ P \left[\begin{array}{ccccc}r _ 1&0&0&{\dots }&0\\ 0& r _ 2&0&{\dots }&0\\
...
..._ k&\lambda _ k ^ 2&{\dots }&\lambda _ k ^ {k-1}\end{array}\right] = \mathcal O$](img144.gif) .
.
Since
![]() are distinct, the van der Monde
matrix has nonzero determinant and so is invertible. We can cancel it
by multiplying both sides on the right by its inverse. Then we get
are distinct, the van der Monde
matrix has nonzero determinant and so is invertible. We can cancel it
by multiplying both sides on the right by its inverse. Then we get
![$ P \left[\begin{array}{ccccc}r _ 1&0&0&{\dots }&0\\ 0& r _ 2&0&{\dots }&0\\
...
...dots }&{\dots }&{\dots }\\ 0&0&0&{\dots }&r _ k\end{array}\right] = \mathcal O$](img145.gif) , or
, or
![]() . Then
. Then
![]() 0 for
each
0 for
each ![]() . Since each
. Since each
![]() 0, we must have
0, we must have ![]() ,
as desired.
,
as desired.