For Problem CC-1:

The transformation is the same as $T(x,y) = (3x-y,-3x+y)$. The range has basis $\left[\begin{array}{r}-1\\ 1\end{array}\right]$. The null space has basis $\left[\begin{array}{r}1\\ 3\end{array}\right]$. The inverse image of $\left[\begin{array}{r}2\\ -2\end{array}\right]$ is the graph of $3x - y = 2$. Graphs are these:

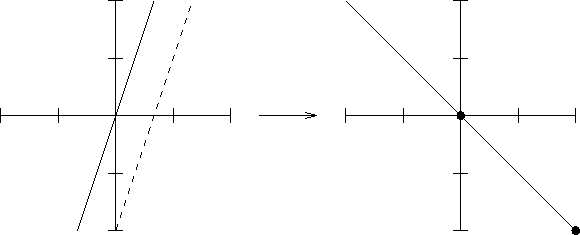
For Problem CC-2: $$\begin{array}{ccccc} T(\cos 2x) &=& -2 \sin 2x &=& 0 \cos 2x ... ...sin 2x) &=& 2 \cos 2x &=& 2 \cos 2x + 0 \sin 2x\\ \end{array}$$ so the matrix is $\left[\begin{array}{cc}0&2\\ -2&0\end{array}\right]$. Notice that this is a scaledrotation: $- 2 R _ {90 ^ \circ}$.

For Problem CC-3:

(a) $p _ A (\lambda) = \lambda ^ 2 - 5 \lambda + 4 = (\lambda - 4)(\lambda - 1)$, so eigenvalues are $\lambda = 4$ and $\lambda = 1$. $A - 4I = \left[\begin{array}{rr}-2&1\\ 2&-1\end{array}\right]$. We could write out equations, but to save effort, notice that we're just looking for a nonzero vector in the null space, or equivalently, a vector perpendicular to both rows, so we can use $\left[\begin{array}{r}1\\ 2\end{array}\right]$ as the eigenvector. $A - I = \left[\begin{array}{rr}1&1\\ 2&2\end{array}\right]$ and a vector perpendicular to both rows is $\left[\begin{array}{r}1\\ -1\end{array}\right]$. Therefore $P^{-1} A P = D$ with $P = \left[\begin{array}{rr}1&1\\ 2&-1\end{array}\right]$ and $D = \left[\begin{array}{rr}4&0\\ 0&1\end{array}\right]$.

(b) Using the same $P$ as in (a) we get $P^{-1} A ^ 2 P = D ^ 2 = \left[\begin{array}{rr}16&0\\ 0&1\end{array}\right]$. It is not even necessary to calculate the entries of $A ^ 2$.

For Problem CC-4:

(a) $P _ A(\lambda) = \lambda ^ 2 - 7 \lambda - 8 = (\lambda - 8)(\lambda + 1)$, so eigenvalues are $\lambda = 8$, $\lambda = -1$. We get $A -8I = \left[\begin{array}{rr}-6&3\\ 6&-3\end{array}\right]$ and (as in the solution to CC-) a vector perpendicular to both rows is $\left[\begin{array}{r}1\\ 2\end{array}\right]$. We get $A - (-1)I = A + I = \left[\begin{array}{rr}3&3\\ 6&6\end{array}\right]$, and a vector perpendicular to both rows is $\left[\begin{array}{r}1\\ -1\end{array}\right]$. Therefore $P^{-1} A P = D$ with $P = \left[\begin{array}{rr}1&1\\ 2&-1\end{array}\right]$ and $D = \left[\begin{array}{rr}8&0\\ 0&-1\end{array}\right]$. Later we'll need $P^{-1}$, which is $\frac 1{-3}\left[\begin{array}{rr}-1&-1\\ -2&1\end{array}\right] = \frac 13 \left[\begin{array}{rr}1&1\\ 2&-1\end{array}\right]$.

(b) We want $B ^ 3 = A$, so if we let $E = P^{-1} B P$ then we'll have $E ^ 3 = D$. We don't know $B$ or $E$ yet, but we can get them by letting $E$ be the cube root of $D$, specifically, $E = \left[\begin{array}{rr}2&0\\ 0&-1\end{array}\right]$ and then setting $B = P E P^{-1} = \left[\begin{array}{rr}1&1\\ 2&-1\end{array}\right] \left[\b... ...end{array}\right] = \dots = \left[\begin{array}{rr}0&1\\ 2&1\end{array}\right]$. This answer can be checked by cubing it.

Incidentally, do you see connections between this problem and Problem CC-?

For Problem CC-5: $(AB) _ {ij} = \sum_k A _ {ik} B _ {kj}$ so trace$(AB) = \sum_i \sum_k A _ {ik} B _ {ki}$, while $(BA) _ {ij} = \sum_k B _ {ik} A _ {kj}$ so trace$(BA) = \sum_i \sum_k B _ {ik} A _ {ki}$. If we switch the order of summation in this second equation and then switch the letters $i$ and $k$, neither of which changes the value, we get the first equation.

For Problem CC-6:

For (a): Say $A$ is invertible. Then $A^{-1} (AB) A = BA$. The case where $B$ is invertible is the same with the letters switched.

(b) It is possible to have $AB = \mathcal O$ and $BA \neq \mathcal O$ (mathcal O meaning zero matrices here): Take $A = \left[\begin{array}{rr}1&0\\ 0&0\end{array}\right]$, $B = \left[\begin{array}{rr}0&0\\ 1&0\end{array}\right]$. The only matrix similar to a zero matrix is the zero matrix itself, so $AB$ and $BA$ can't be similar.

For Problem CC-7:

(a) The characteristic polynomial of $A$ is $\lambda ^ 2 - t \lambda + \Delta$, where $t =$   trace$\; A$ and $\Delta =$   det$\; A$. But $t$ is also the sum of the eigenvalues and $\Delta$ is also the product of the eigenvalues, so $t = 1$ and $\Delta = -1$, and $p _ A(\lambda) = \lambda ^ 2 - \lambda - 1$. From here there are two approaches:

(i) a diagonal matrix as the solution: Solving with the quadratic equation, we find that the eigenvalues are $\lambda = {\frac 1 2}(1 \pm \sqrt 5)$, so an answer is $A = \left[\begin{array}{cc}{\frac 1 2}(1 + \sqrt 5)&0\\ 0&{\frac 1 2}(1 - \sqrt 5)\end{array}\right]$.

(ii) (easier) just invent a matrix with the proper trace and determinant. For diagonal entries take $1,0$. For off-diagonal entries to make the determinant come out right, take $1,1$. So an answer is $A = \left[\begin{array}{rr}1&1\\ 1&0\end{array}\right]$.

Note: In a problem of this kind, you can always take one diagonal entry to be 0 and still be sure of finding other entries that will work.

(b) One way: $R _ \theta = \left[\begin{array}{rr}\cos \theta& -\sin \theta\\ \sin \theta& \cos \theta\end{array}\right]$. We know $\sin \theta = 0$ for $\theta = 0$ and $\theta = \pi$. The first of these is excluded, and the other gives $A = \left[\begin{array}{rr}-1&0\\ 0&-1\end{array}\right] = -I$.

A better way: A rotation matrix is characterized by having orthonormal columns and determinant 1. In a diagonal matrix the columns are already perpendicular; to be orthonormal the diagonal entries should be $\pm 1$. To get determinant 1, they should both be 1 or both be $-1$. The first is excluded, so the only possible answer is $-I$.

(c) This problem mentions Cayley's Theorem, which we'll discuss in class: Theorem: For any $n \times n$ matrix $A$, $p _ A(A)$ is the $n \times n$ zero matrix. Working as in (a)-(ii), let the diagonal entries be $1,0$ and the off-diagonal entries be $1,-1$, so the matrix is $A = \left[\begin{array}{rr}1&1\\ -1&0\end{array}\right]$. It can be checked that $A$ works. (The method (a)-(i) is also OK, but this time the eigenvalues are complex.)

Incidentally, recalling the polynomial factorization $x ^ 3 - 1 = (x-1)(x ^ 2 - x + 1)$, we see that for this $A$ we have $A ^ 3 - I = (A - I)(A ^ 2 - A + I) = 0$ (the zero matrix), so $A ^ 3 = I$. For the same reason, the eigenvalues of $A$ must be complex cube roots of 1, which are studied in Math 132.

(d) The simplest examples would be to take $A$ to be the $2 \times 2$ identity matrix and $\lambda = 1$, or the $2 \times 2$ zero matrix and $\lambda = 0$; the eigenspace is the whole space either way. If the problem had asked for a $3 \times 3$ example, it's still simplest to use a diagonal matrix: $A = \left[\begin{array}{rrr}1&0&0\\ 0&1&0\\ 0&0&0\end{array}\right]$ and $\lambda = 1$, or $A = \left[\begin{array}{rrr}0&0&0\\ 0&0&0\\ 0&0&1\end{array}\right]$ and $\lambda = 0$; the eigenspace is the $x,y$-plane in either case.

For Problem CC-8:

(a) We might as well try for the $n$-cycle $\left(\begin{array}{rrrr}1&2&{\dots }&n\end{array}\right)$, so $1 \mapsto 2 \mapsto \dots \mapsto n \mapsto 1$. Let's start with $(1 \; 2)$. This takes 1 to 2, which is good, but 2 to 1, which is bad. To get 2 to go to 3, follow with $(1 \; 3)$, on the left since we are composing functions. So far we have $(1 \; 3) (1 \; 2)$. This takes 1 to 2 and 2 to 3 but 3 to 1, so follow with $(1 \; 4)$, and so on. Therefore one answer is $(1 \; n) (1 \; (n-1)) \dots (1 \; 3) (1 \; 2)$. More generally, if symbols are $a _ 1,\dots, a _ n$, we have $(a _ 1 \; a _ n) (a _ 1 \; a _ {n-1}) \dots (a _ 1 \; a _ 2) = \left(\begin{array}{rrrr}a _ 1&a _ 2&{\dots }& a _ n\end{array}\right)$.

Incidentally, when we say ``and so on'', we are really using informal induction. That's appropriate for small proofs like this one, as long as we know how to make it formal if required. The induction step here would involve checking that $\left(\begin{array}{rr}1&n\end{array}\right) \left(\begin{array}{rrrr}1&2&{\do... ...-1)\end{array}\right) \left(\begin{array}{rrrr}1&2&{\dots }&n\end{array}\right)$. In this course there wasn't much practice with induction, so you will not be expected to use it in unfamiliar contexts like this one.

For another answer, first start with a naive attempt: $(1 \; 2) (2 \; 3) \dots ((n-1) \; n)$. This has two drawbacks: First, it involves thinking from left to right, instead of right to left, and second, it gives the undesired answer $\left(\begin{array}{rrrr}1&n&{\dots }&2\end{array}\right)$. But that is an $n$-cycle, so in a sense it has solved the problem, even if awkwardly. We can fix up this idea by looking at it and reversing the appearances of $n,{\dots },2$, while leaving the appearance of 1 alone. We get

$(1 \; n) ((n-1) \; (n-2)) \dots (3 \; 2) = \left(\begin{array}{rrrr}1&2&{\dots }&n\end{array}\right)$ as desired. More generally, $(a _ 1 \; a _ n) (a _ {n-1} \; a _ {n-2}) \dots (a _ 3 \; a _ 2) = \left(\begin{array}{rrrr}a _ 1&a _ 2&{\dots }& a _ n\end{array}\right)$.

(b) As stated, every permutation is a product of disjoint cycles, and by (a) every cycle is a product of transpositions, so every permutation is a product of transpositions.

It is also possible to prove (b) directly. Take a permutation $\sigma$. Imagine doing $\sigma$ to a deck of cards numbered $1,2,\dots, n$, so they're all out of order. Can you put them back in order using transpositions? Yes: Wherever card 1 is, switch it to the top. Then switch card 2 to the second position from the top, etc. When you're done the deck will be in order. In other words, you have accomplished $\sigma^{-1}$ by doing a product of $n-1$ transpositions, say $\sigma^{-1} = \tau _ {n-1}\dots \tau _ 1$, where the $\tau _ i$ are transpositions. Then $\sigma = (\tau _ {n-1}\dots \tau _ 1) ^ {-1} = \tau _ 1^{-1}\dots \tau _ {n-1}^{-1}$ (reversing just like inverting a product of matrices), and since each transposition is its own inverse this shows $\sigma = \tau _ 1\dots \tau _ {n-1}$.

(c) In $S _ 3$, $\mathbf{1}$ and the two 3-cycles are even; the three transpositions are odd. As stated it can be checked that even times even or odd times odd is even, while even times odd or odd times odd is odd.

For Problem CC-9:

(a) Since these are separate DE's, $x(t) = x(0) e^{4t} = e^{4t}$ and $y(t) = y(0) e ^ {-7t} = 2 e ^ {-7t}$.

(b) x$' = D$   x with $D = \left[\begin{array}{rr}4&0\\ 0&-7\end{array}\right]$ and x$(0) = \left[\begin{array}{r}1\\ 2\end{array}\right]$.

(c) x$(t) = e ^ {Dt}$   x$(0)$ says $\left[\begin{array}{r}x\\ y\end{array}\right] = \left[\begin{array}{rr}e ^ {4... ...\\ 0&e ^ {-7t}\end{array}\right]\left[\begin{array}{r}1\\ 2\end{array}\right]$, the same as (a).

(d) If x$(t) = e ^ {Dt}$x$(0)$, differentiating and assuming that ordinary rules apply, we get x$'(t) = D e ^ {Dt}$x$(0) = D$x$(t)$, and clearly setting $t=0$ we do get x$(0)$ as the value.

Note: Since $e ^ {Dt}$ involves terms that are all powers of $D$, it commutes with $D$, so it doesn't matter whether we write $D e ^ {Dt}$ or $e ^ {Dt} D$, but the first of these fits better here.

For Problem CC-10:

(a) To summarize: $P^{-1} A P = D$ with $D = \left[\begin{array}{rr}5&0\\ 0&1\end{array}\right]$ and $P = \left[\begin{array}{rr}1&1\\ 1&-1\end{array}\right]$, $P^{-1} = {\frac 1 2}\left[\begin{array}{rr}1&1\\ 1&-1\end{array}\right]$. Substituting x$= P$z we get $(P$z$)' = A P$z, which is the same as $P$z$' = A P$z (since the derivative of a vector means the vector of derivatives, and since we are multiplying by the constant matrix $P$). Putting $P$ on the right we get z$' = P^{-1} A P$z, or z$' = D$z, which has the solution $z(t) = z(0) e ^ {5t}$, $w(t) = w(0) e ^ t$. But what are these initial values? We had x$= P$z, so z$= P^{-1}$   x, $\left[\begin{array}{r}z(0)\\ w(0)\end{array}\right] = {\frac 1 2}\left[\begin... ...d{array}\right] = \left[\begin{array}{r}\frac 32\\ -\frac 12\end{array}\right]$. The solution, then, from x$= P$   z, is $\left[\begin{array}{r}x\\ y\end{array}\right] = \left[\begin{array}{rr}1&1\\ ... ...t] \left[\begin{array}{r}\frac 32 e ^ {5t}\\ -\frac 12 e ^ t\end{array}\right]$, or $x = \frac 32 e ^ {5t} - {\frac 1 2}e ^ t$, $y = \frac 32 e ^ {5t} + {\frac 1 2}e ^ t$. This checks in the original DE.

In matrix form the answer is x$= P e ^ {Dt} P^{-1}$   x$(0)$.

(b) The matrix power answer ought to be x$(t) = e ^ {At}$   x$(0)$. Inventing reasonable rules, the derivative of the right-hand side is $A e ^ {At}$x$(0) = A$x$(t)$, so that checks.

Note: This answer and the previous answer are consistent: Because $e ^ {Dt}$ is an infinite sum of scaled powers of $Dt$, and because similarity by a fixed $P$ preserves matrix multiplication and addition, we get $P e ^ {Dt} P^{-1} = e ^ {P Dt P^{-1}} = e ^ {At}$.