For Problem E-1:
Method #1: If
![]() 0, expanding and
then regrouping we get
0, expanding and
then regrouping we get
![]() 0. Since
0. Since
![]() are linearly independent, these coefficients must be
0, so
are linearly independent, these coefficients must be
0, so
![]() . Working backwards from
. Working backwards from
![]() we get
we get ![]() ,
, ![]() . Therefore
. Therefore
![]() 0 implies
0 implies
![]() , and so
, and so
![]() are linearly independent.
are linearly independent.
Method #2: The subspace ![]() of
of ![]() generated by
generated by ![]() is isomorphic to
is isomorphic to ![]() with
with ![]() corresponding to
corresponding to
![]() , since
, since ![]() span it and are linearly
independent. Under this isomorphism,
span it and are linearly
independent. Under this isomorphism,
![]() correspond to
correspond to
![]() . Making these the
rows of a matrix and row-reducing we get the identity matrix,
which has rank 3, so they must be linearly independent. Using
the isomorphism,
. Making these the
rows of a matrix and row-reducing we get the identity matrix,
which has rank 3, so they must be linearly independent. Using
the isomorphism,
![]() must be linearly independent.
must be linearly independent.
For Problem E-2:
Using the augmented matrix and row reducing,
![$ \left[\begin{array}{rrrrr}1&0&1&0&0\ 0&0&1&1&0\ 1&1&0&1&0\ 0&1&1&0&1\end...
...&0&0\ 0&1&1&1&0\ 0&0&1&1&0\ 0&0&0&1&1\end{array}\right] \rightsquigarrow $](img212.gif)
![$ \left[\begin{array}{rrrrr}1&0&0&1&0\ 0&1&0&0&0\ 0&0&1&1&0\ 0&0&0&1&1\end...
...rray}{rrrrr}1&0&0&0&1\ 0&1&0&0&0\ 0&0&1&0&1\ 0&0&0&1&1\end{array}\right],$](img213.gif) from which we see there is the unique solution
from which we see there is the unique solution
![]() . This checks.
. This checks.
For Problem E-3:
![$ M = \left[\begin{array}{rrrrr} 1& 2& 1& 3& -2\ 1& 2& 2& 3& 0\ 1& 2& 3& 3& ...
...left[\begin{array}{rrrrr}1&2&0&3&-4\ 0&0&1&0&2\ 0&0&0&0&0\end{array}\right]$](img215.gif) .
.
The two nonzero rows of ![]() are a basis for the row space.
are a basis for the row space.
For the null space, we write the general solution in variables,
say,
![]() , getting
, getting
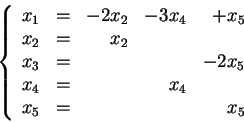
so
![$ \left[\begin{array}{c}x_1\ x_2\ x_3\ x_4\ x_5\end{array}\right] = x_2 ...
...ay}\right] + x_5 \left[\begin{array}{r}1\ 0\ -2\ 0\ 1\end{array}\right]$](img218.gif) . These three column vectors
are then the basis.
. These three column vectors
are then the basis.
For the column space, we look at ![]() and see that the pivot
columns are columns 1 and 3, so a basis for the column space is
columns 1 and 3 of
and see that the pivot
columns are columns 1 and 3, so a basis for the column space is
columns 1 and 3 of ![]() . (Alternatively, we could transpose
. (Alternatively, we could transpose ![]() ,
row reduce, and take the resulting nonzero rows.)
,
row reduce, and take the resulting nonzero rows.)
For Problem E-4:
(a) one-to-one and onto; (b) neither; (c) onto; (d) neither; (e) one-to-one.
For Problem E-5:
If
![]() in
in ![]() , is
, is
![]() ? Since
? Since
![]() is onto we know
is onto we know
![]() ,
,
![]() , for
some
, for
some
![]() ; we must have
; we must have
![]() or else we
would have
or else we
would have
![]() .
.
![]() are defined to
be
are defined to
be ![]() , so the answer is yes. Therefore
, so the answer is yes. Therefore ![]() is one-to-one.
is one-to-one.
If ![]() is there some
is there some ![]() with
with ![]() ? Yes,
? Yes,
![]() works. So
works. So ![]() is onto.
is onto.
For Problem E-6:
First, some notation: If we have a function like
![]() given
by
given
by
![]() and we want to describe it without naming it,
we can just write
and we want to describe it without naming it,
we can just write
![]() , which we say as ``
, which we say as ``![]() maps
to
maps
to ![]() ''. The different-looking arrow is a reminder that
we're talking about elements rather than whole spaces. But sometimes
it's handy to use this kind of notation with the name of a function;
for example, instead of ``Let
''. The different-looking arrow is a reminder that
we're talking about elements rather than whole spaces. But sometimes
it's handy to use this kind of notation with the name of a function;
for example, instead of ``Let ![]() '' we can say ``Let
'' we can say ``Let
![]() '', read as ``
'', read as ``![]() maps to
maps to ![]() under
under ![]() '' or
``via
'' or
``via ![]() ''.
''.
In this notation, if
![]() is a one-to-one correspondence
then
is a one-to-one correspondence
then
![]() is the same as
is the same as
![]() .
.
The same notation can be used to to express the idea that a
linear transformation
![]() preserves addition of vectors:
preserves addition of vectors:
Instead of
![]() we can say
we can say
``If
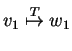 and
and
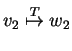 then
then
 .''
.''
To say that ![]() preserves multiplication by scalars, we can say
preserves multiplication by scalars, we can say
``If
![]() then
then
![]() ,
for any
,
for any ![]() ''.
''.
Now to do the problem: To check that ![]() preserves addition,
we must show that for any
preserves addition,
we must show that for any
![]() if
if
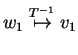 and
and
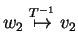 then
then
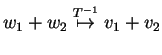 . But this is exactly
the same as saying that if
. But this is exactly
the same as saying that if
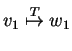 and
and
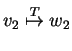 then
then
 , which is true since
, which is true since ![]() preserves addition. Therefore
preserves addition. Therefore ![]() preserves addition.
preserves addition.
Similarly, to check multiplication by scalars, if
![]() then we want
then we want
![]() .
But this is the same as
.
But this is the same as
![]() , which is true
since
, which is true
since ![]() preserves multiplication by scalars.
preserves multiplication by scalars.
Therefore ![]() is an isomorphism.
is an isomorphism.
For Problem E-7:
In (b), with the basis ![]() for
Pols
for
Pols![]() there
is an isomorphism
there
is an isomorphism
![]() Pols
Pols![]() taking
taking
![]() to
to ![]() . Under this isomorphism, part (b) becomes part (a),
so the span is the whole space.
. Under this isomorphism, part (b) becomes part (a),
so the span is the whole space.
(c) In (c), using the basis ![]() for
Pols
for
Pols![]() ,
the resulting isomorphism with
,
the resulting isomorphism with
![]() turns part (c) into part (a),
so the span is the whole space.
turns part (c) into part (a),
so the span is the whole space.
For Problem E-8:
For (a):
(ii) says the pivot columns of ![]() are columns 1, 3, and 5.
are columns 1, 3, and 5.
(iii) expresses the other columns as linear combinations of the
pivot columns. Therefore columns 2, 4, and 6 are
![$ \left[\begin{array}{r}3\ 0\ 0\end{array}\right]$](img260.gif) ,
,
![$ \left[\begin{array}{r}2\ 5\ 0\end{array}\right]$](img261.gif) , and
, and
![$ \left[\begin{array}{r}-1\ 7\ -4\end{array}\right]$](img262.gif) .
.
Putting these together says that the mystery matrix is
![$ M = \left[\begin{array}{rrrrrr}1&3&0&2&0&-1\ 0&0&1&5&0&7\ 0&0&0&0&1&-4\end{array}\right]$](img263.gif) .
.
For (b): Knowing the linear relations means we know which columns are linear combinations of preceding columns, and what the coefficients are. So just as for the mystery matrix, if we are given any matrix in row-reduced echelon form, the pivot columns are those which are not the in the span of the preceding columns; these columns look like some columns of the identity matrix, in order. Each remaining column is a linear combination of the preceding pivot columns, and the coefficients tell its entries.
For (c): Suppose ![]() is row-reduced by two people to matrices
is row-reduced by two people to matrices
![]() and
and ![]() in row-reduced echelon form. Both
in row-reduced echelon form. Both ![]() and
and ![]() have the same linear relations between columns as
have the same linear relations between columns as ![]() does and so have the same linear relations between columns as
each other. But by (b) we know these linear relations uniquely
determine the entries of
does and so have the same linear relations between columns as
each other. But by (b) we know these linear relations uniquely
determine the entries of ![]() and
and ![]() , so that
, so that ![]() .
Therefore the row-reduced echelon form is unique.
.
Therefore the row-reduced echelon form is unique.