Assignment #10

No quiz this week. Homework due Friday, November 30: These include a couple of topics that will be discussed 10-M and 10-W (Jordan canonical form and determinants.)

where	Do but don't hand in	Hand in
DD	DD-11	DD-10
EE	EE-1, EE-2, EE-5, EE-6, EE-8, EE-10	EE-3, EE-4, EE-7,
	EE-11, EE-12, EE-13, EE-14, EE-15, EE-16	EE-9, EE-17(a)-(c)
FF	FF-1, FF-2

Problem EE-1. For the theorem that eigenvectors for distinct eigenvalues are linearly independent, in class we used an informal induction. Write out a proof using a formal induction. Method:

• Write down a clear statement of what is to be proved.

  (This will be some statement depending on an integer parameter. In the present problem, we are discussing $k$ eigenvectors of an $n \times n$ matrix, and it's $k$ that is the parameter. The proof doesn't mention $n$.)

• Prove the statement for the lowest case (usually $k = 1$ or $k = 0$). Often this is trivial.

• Prove the statement for the case of general $k$, assuming that it is true for the case $k-1$. (This assumption is the ``inductive hypothesis''.)

• End by saying, ``Therefore the statement is true for all $k$ by mathematical induction.''

Note. Usually a proof by induction involves some statement $P(k)$ that is to be proved infinitely many values of $k$. In the present problem, though, $k$ goes up only to $n$, or to however many distinct eigenvalues there are if there are fewer than $n$ distinct values. For more on induction, see the link on our course home page.

Problem EE-2. What is wrong with the following ``proof'' that all cows are the same color?

``Statement: Any $k$ cows are the same color, for $k= 1, 2, \dots$ Proof by induction: The case $k = 1$ is trivially true. Assume the case $k-1$ holds, and consider $k$ cows. Line them up. By the inductive hypothesis, the first $k-1$ are the same color and so are the last $k-1$. Since the first $k-1$ and the last $k-1$ overlap in the middle, all the cows must be the same color.''

Problem EE-3. (a) Show that if a matrix $M$ commutes with a diagonal matrix $D$ whose diagonal entries are distinct, then $M$ is also diagonal.

(b) Show that if a matrix $B$ commutes with a diagonalizable matrix $A$ that has no repeated eigenvalues (i.e.,whose eigenvalues are distinct), then $B$ is also diagonalizable. In fact, show that $A$ and $B$ are simultaneously diagonalizable (meaning that the same $P$ can be used for both). (Method: Remember, the map $M \mapsto P^{-1} M P$ preserves multiplication.)

Problem EE-4. In finding a square root for $A = \left[\begin{array}{rr}5&4\\ 4&5\end{array}\right]$ we discussed how to get four answers. Are there any other answers--at least, are there any other answers that are diagonalizable?

(Method: This time we must show that if $B^2 = A$ then $B$ is one of four possibilities. The proof will sound like the original construction, but the reasoning is a little different: Start by diagonalizing $A$ using some $P$. Leave $P$ unchanged throughout the rest of the problem. Let $E = P^{-1} B P$. Then $E^2 = D$. (Why?) Use Problem EE- to show that $E$ is diagonal, and then discuss the possibilities for $E$. If you can pin $E$ down, then $B$ is uniquely determined by $E$ since $B = P E P^{-1}$.)

Problem EE-5. Make up an example as though you were tutoring a Math 115A student, as follows:

(a) Invent a $2 \times 2$ matrix $A$ with nonzero integer entries so that $A$ can be diagonalized using $P$ for which both $P$ and $P^{-1}$ have only integer entries.

(b) Make up a simultaneous DE problem using $A$ and solve it.

Problem EE-6. Diagonalize the matrix $R _ {90 ^ \circ}$ over $\mathbb{C}$.

Problem EE-7. As in Problem EE-, to diagonalize a matrix it may be necessary to work in a larger field. Show that this is the case for the matrix $A = \left[\begin{array}{rr}1&1\\ 1&0\end{array}\right]$ over GF(2). Specifically, show that $A$ is not diagonalizable over GF(2), but is diagonalizable over a larger field.

Problem EE-8. Using Jordan canonical form, explain why it's obvious that a matrix with distinct eigenvalues is diagonalizable.

Problem EE-9. A matrix $A$ is a projection if $A^2 = A$. For example, $A = \left[\begin{array}{rr}1&0\\ 0&0\end{array}\right]$ is a projection, as are any size identity matrix and any size square zero matrix. Show that any projection is diagonalizable. (Method: Use Jordan canonical form.)

Problem EE-10. Invent a real $2 \times 2$ matrix $A$ such that $A^2 = A + I$. (Method: Use Cayley's theorem.)

Problem EE-11. Using the fact that the volume of a sphere of unit radius is $\frac 43 \pi$, find a formula for the volume of an ellipsoid with semimajor axes $a,b,c$.

Problem EE-12. How is the determinant of a permutation matrix related to the sign of the permutation (which means 1 for even, $-1$ for odd)? Explain.

Problem EE-13. For finding the determinant of a $10 \times 10$ matrix, compare the number of multiplications involved in using the permutation definition of a determinant, versus the number involved in finding the determinant using elementary row operations. (Approximate numbers are OK.)

Problem EE-14. Suppose that there are three containers, containing respectively a red marble, a blue marble, and a green marble. The tops of the containers are labeled $R, B, G$. However, all the labels are wrong! How many containers do you have to look inside before you know the correct contents of all three containers?

Problem EE-15. For $S_4$, the set of permutations on four symbols, what kinds of cycle decompositions are possible? Which are even and which are odd? (It is not necessary to list all 24 permutations, just the possible forms of cycles, e.g., $\left(\begin{array}{rrr}a&b&c\end{array}\right)$, meaning any 3-cycle.)

Problem EE-16. What is the change-of-basis matrix in each of the following cases?

(a) $V = \mathbb{R}^ 3$. The old basis is the standard basis; the new basis consists of $v _ 1 = (1,1,1)$, $v _ 2 = (1,1,-2)$, $v _ 3 = (1,2,1)$.

(b) Same as (a) with old and new switched.

(c) $V$ is the subspace of $\mathbb{R}^ 3$ that is the solution space of $x+y+z = 0$. The old basis consists of $v _ 1 = (1,-1,0)$, $v _ 2 = (1,0,-1)$; the new basis consists of $w _ 1 = (1,-1,0)$, $w _ 2 = (1,1,-2)$.

(d) $V = \mathbb{R}^ n$ and $A$ is a diagonalizable $n \times n$ real matrix. The old basis is the standard basis; the new basis consists of linearly independent eigenvalues $v _ 1,\dots, v _ n$.

(e) $V =$   Pols$(\mathbb{R}, 2)$. The old basis is $1, x, x^2$; the new basis is $1, 1+x, 1+x+x^2$.

Problem EE-17. A van der Monde matrix is a square matrix of the form $\left[\begin{array}{ccccc} 1&x _ 1& x _ 1 ^ 2&{\dots }&x _ 1 ^ {n-1}\\ {\dot... ...dots }&{\dots }\\ 1&x _ n& x _ n ^ 2&{\dots }&x _ n ^ {n-1}\end{array}\right]$, where $x _ 1,\dots, x _ n \in F$ for a field $F$.

A van der Monde determinant is the determinant of a van der Monde matrix. It has a nice value:

Theorem. The van der Monde determinant 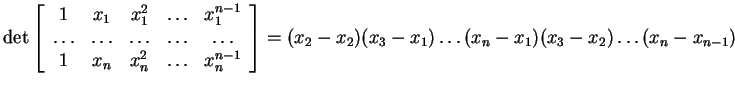$\det \left[\begin{array}{ccccc} 1&x _ 1& x _ 1 ^ 2&{\dots }&x _ 1 ^ {n-1}\\ ... ...2)(x _ 3 - x _ 1)\dots (x _ n - x _ 1)(x _ 3 - x _ 2) \dots (x _ n - x _ {n-1})$, or better,

$$\prod_{i<j} (x _ j - x _ i),$$

taken over all $i, j \in \{1,\dots, n\}$ with $i < j$. For example, for $n = 3$ we get $(x _ 2 - x _ 1)(x _ 3 - x _ 1) (x _ 3 - x _ 2)$.

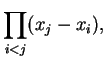
(a) What is the value of the $3 \times 3$ van der Monde determinant with $x _ 1 = 100$, $x _ 2 = 101$, $x _ 3 = 102$?

(b) If $x _ 1,\dots, x _ n$ are distinct then the van der Monde matrix is invertible. Explain why. (Easy.)

(c) Explain why there must be a unique parabola $y = c _ 0 + c _ 1 x + c _ 2 x^2$ through the three data points $(2,8), (3,7), (5,1)$.

(Method: Set this up as equations with $c _ 0, c _ 1, c _ 2$ as unknowns. You are not asked to solve the equations. Interestingly, even though we are talking about a parabola, the equations are linear, because the coefficients of a quadratic appear linearly!)

(d) Use the Theorem to re-prove the theorem that eigenvectors for distinct eigenvalues are linearly independent, without using induction.

(Method: Take the equation $r _ 1 v _ 1 + \dots + r _ k v _ k =$   0, in which you are hoping to show the coefficients are all 0. Apply $\tau _ A$ repeatedly to get $n-1$ more equations, of which the last is $\lambda _ 1 ^ {k-1} r _ 1 v _ 1 + \dots + \lambda _ k ^ {k-1} r _ k =$   0. As you know, the first equation can be rewritten as $P$   r$=$   0, where $P$ is an $n \times k$ matrix with columns $v _ 1,\dots, v _ k$ and r$= \left[\begin{array}{c}r _ 1\\ \dots \\ r _ k\end{array}\right]$. Rewrite the other equations the same way, using $P$ but fancier things in place of r. Put r and the fancier things as columns of a matrix $H$, so $PH = \mathcal O$ (the zero matrix). Then factor $H$ as a diagonal matrix with diagonal entries $r _ 1,\dots, r _ k$ times a van der Monde matrix. Since the van der Monde matrix is invertible you can cancel it. Then what?)