Quiz 9 in discussion section Tuesday, November 27:
For a linear transformation
![]() between vectors spaces
and a subspace
between vectors spaces
and a subspace ![]() of
of ![]() , (a) be able to define what
, (a) be able to define what
![]() means, and (b) be able to prove that
means, and (b) be able to prove that ![]() is a subspace of
is a subspace of ![]() . (See Problem O-3 and its solution.)
. (See Problem O-3 and its solution.)
Assignment due Friday, November 30.
| where | Do but don't hand in | Hand in |
| U | 7 | |
| CC | CC-1, CC-6, CC-7, CC-8, CC-9 | CC-2, CC-3, CC-4, CC-5, CC-10 |
| DD | DD-1, DD-3, DD-5, DD-7 | DD-2, DD-4, DD-6, DD-8, DD-9 |
Problem
CC-1. For the linear transformation
![]() R
R![]() R
R![]() with
with
![$ A = \left[\begin{array}{rr}3&-1\\ -3&1\end{array}\right]$](img9.gif) , sketch (a) the range, (b) the null space, and
(c) the inverse image of
, sketch (a) the range, (b) the null space, and
(c) the inverse image of
![$ \left[\begin{array}{r}2\\ -2\end{array}\right]$](img10.gif) [the set of vectors in the
domain that go to this vector]. Use two sets of axes. Do a
careful job, indicating the scale by ``tick marks'' on the axes.
Label your answers.
[the set of vectors in the
domain that go to this vector]. Use two sets of axes. Do a
careful job, indicating the scale by ``tick marks'' on the axes.
Label your answers.
Problem
CC-2. Let ![]() be the solution space of the DE
be the solution space of the DE ![]() . Let
. Let
![]() be the basis consisting of
be the basis consisting of
![]() . If
. If
![]() is the differentiation operator, find the matrix of
is the differentiation operator, find the matrix of ![]() relative to this basis.
relative to this basis.
Problem
CC-3. (a) Diagonalize the matrix
![$ A = \left[\begin{array}{rr}2&1\\ 2&3\end{array}\right]$](img16.gif) . Be sure to
give
. Be sure to
give ![]() and
and ![]() , but you don't need to find
, but you don't need to find ![]() .
.
(b) Diagonalize ![]() . (Again, give
. (Again, give ![]() .)
.)
Problem
CC-4. (a) Diagonalize
![$ A = \left[\begin{array}{rr}2&3\\ 6&5\end{array}\right]$](img21.gif) , showing the
matrices involved, with explicit entries, including finding a matrix
inverse where needed. Show that your answer checks, by multiplying
out.
, showing the
matrices involved, with explicit entries, including finding a matrix
inverse where needed. Show that your answer checks, by multiplying
out.
(b) Find a matrix ![]() with
with ![]() .
.
(Method: Diagonalize ![]() using an appropriate
using an appropriate ![]() , take a
cube root, and ``undiagonalize'' by doing a similarity back using
, take a
cube root, and ``undiagonalize'' by doing a similarity back using
![]() in place of
in place of ![]() .)
.)
Problem
CC-5. Show that for an
![]() matrix
matrix
![]() and
and
![]() matrix
matrix ![]() over the same field,
trace
over the same field,
trace![]() trace
trace![]() .
.
Problem
CC-6. (a) Show that square matrices ![]() of the same size, if at
least one of
of the same size, if at
least one of ![]() and
and ![]() is invertible (i.e., nonsingular) then
is invertible (i.e., nonsingular) then
![]() and
and ![]() are similar. (Method: Easy matrix manipulation.)
are similar. (Method: Easy matrix manipulation.)
(b) Looking through past homework, find an example to show
that (a) might not hold if neither of ![]() and
and ![]() is invertible.
(Method: What if
is invertible.
(Method: What if ![]() ?)
?)
Problem CC-7. Invent a specific numeric example of each of the following, giving a brief reason in each case:
(a) A
![]() matrix with eigenvalues whose sum is 1 and
whose product is
matrix with eigenvalues whose sum is 1 and
whose product is ![]() .
.
(b) A
![]() diagonal matrix that is a rotation but is not the
identity matrix.
diagonal matrix that is a rotation but is not the
identity matrix.
(c) A matrix ![]() such that
such that
![]() . (Method: Just
find a
. (Method: Just
find a
![]() matrix
matrix ![]() with characteristic polynomial
with characteristic polynomial
![]() . Magically, any matrix acts like
a root of its own characteristic polynomial. Check your answer.)
. Magically, any matrix acts like
a root of its own characteristic polynomial. Check your answer.)
(d) A matrix ![]() and eigenvalue
and eigenvalue ![]() so that the eigenspace
so that the eigenspace
![]() has dimension 2.
has dimension 2.
Problem
CC-8. By ``permutation'' we will always mean a permutation on a
finite number of symbols. Recall that a transposition means a
2-cycle such as
![]() .
.
(a) Show that the n-cycle
![]() is a product
of transpositions. In other words, you can achieve an
is a product
of transpositions. In other words, you can achieve an ![]() -cycle
by switching two symbols at a time, several times. (Advice:
Try this for
-cycle
by switching two symbols at a time, several times. (Advice:
Try this for ![]() , then
, then ![]() , etc. until you see a
general method.)
, etc. until you see a
general method.)
(b) Show that every permutation is a product of transpositions. (Quote the fact that every permutation is a product of ``disjoint'' cycles and use (a).)
(c) A permutation ![]() is said to be even if
is said to be even if ![]() is
the product of an even number of transpositions, or odd if
is
the product of an even number of transpositions, or odd if
![]() is the product of an odd number of transpositions.
is the product of an odd number of transpositions.
It is a fact that any permutation is either even or odd, but not both.
Looking at the multiplication table for ![]() (p. AA
3), say which permutations are even, which are odd, and check
that a transposition times an even permutation is odd and vice
versa. (It may help to draw a horizontal line and vertical line
to split the table into four areas.)
(p. AA
3), say which permutations are even, which are odd, and check
that a transposition times an even permutation is odd and vice
versa. (It may help to draw a horizontal line and vertical line
to split the table into four areas.)
Problem
CC-9. (a) For functions
![]() ,
solve the system of differential equations (DE's)
,
solve the system of differential equations (DE's)
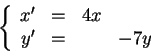 with
with ![]() ,
, ![]() .
.
(Method: Recall that for a single dependent variable the
solution of ![]() is
is
![]() .)
.)
(b) Rewrite the problem in matrix form.
(Method:
x![]() x with
x
x with
x![]() . What is
. What is ![]() ?)
?)
(c) Show that the solution can be expressed in matrix form using
a matrix power, as in Problem W-2, except that the initial values
become a vector on the right:
x![]() x
x![]() .
.
(d) Check the solution directly by taking the derivative of a
matrix power that is a function of ![]() , inventing any
reasonable rules you need for derivatives of matrix functions
of
, inventing any
reasonable rules you need for derivatives of matrix functions
of ![]() .
.
Problem
CC-10. Solve the system of DE's
x![]() x where
x where
![$ A =
\left[\begin{array}{rr}3&2\\ 2&3\end{array}\right]$](img57.gif) and
x
and
x![$ (0) = \left[\begin{array}{r}1\\ 2\end{array}\right]$](img58.gif) , two ways:
, two ways:
(a) by using similarity;
(b) by using a matrix power.
(Methods: For (a) diagonalize ![]() by
by
![]() and substitute
x
and substitute
x![]() z, where
z
z, where
z![$ = \left[\begin{array}{r}z\\ w\end{array}\right]$](img61.gif) . Use algebra to get the system of
DE's
z
. Use algebra to get the system of
DE's
z![]() z and also find
z
z and also find
z![]() . Solve this diagonal
system and then put things back in terms of
x. The solution
does not have to be in matrix form.
. Solve this diagonal
system and then put things back in terms of
x. The solution
does not have to be in matrix form.
For (b) just propose a solution and then check it by taking the
derivative, inventing any needed rules as in the problem
CC-![]() .)
.)