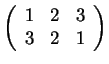 .
.
For Problem V-11:
Starting from the right,
![]() , so the answer is
, so the answer is
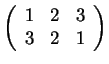 .
.
For Problem V-12:
![]() since going right to left,
since going right to left,
![]() .
.
![]() since
since
![]() . Therefore they do not commute.
. Therefore they do not commute.
Since the particular symbols do not really matter and since
![]() , we see that two transpositions that have just
one symbol in common do not commute; instead their products are
give distinct 3-cycles.
, we see that two transpositions that have just
one symbol in common do not commute; instead their products are
give distinct 3-cycles.
For Problem V-13:
(This problem had a misprint: the last 4 should be 1.)
![]() ,
,
![]() , and
, and
![]() , so the ``cycle decomposition'' is
, so the ``cycle decomposition'' is
![]() .
.
For Problem V-14:

Note: For ![]() the table would be
the table would be
![]() , and
some elements would be non-cycles such as
, and
some elements would be non-cycles such as ![]() .
.