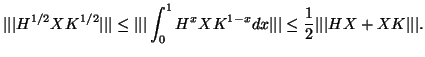One-parameter versions of the Heinz inequality
The celebrated Heinz inequality ([6]) states
where 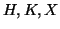 are Hilbert space operators with
are Hilbert space operators with
 .
This estimate actually remains valid for arbitrary unitarily
invariant norms
.
This estimate actually remains valid for arbitrary unitarily
invariant norms
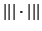 , and in the recent years such
norm inequalities for various operator means have been
investigated by several authors. For example, the following
arithmetic-logarithmic-geometric mean inequality ([7])
is known:
, and in the recent years such
norm inequalities for various operator means have been
investigated by several authors. For example, the following
arithmetic-logarithmic-geometric mean inequality ([7])
is known:
Firstly, the general theory on operator means worked out in [8,9])
is reviewed, which is built upon the theory of Stieltjes double integral
transformations ([4]). It enables us to associate operator means to
certain scalar means and moreover to establish norm comparison results as
above in a unified fashion.
Secondly, as applications several norm inequalities involving quantities
such as
![$\displaystyle \vert\vert\vert H^{\frac{1+\alpha}{2}}XK^{\frac{1-\alpha}{2}}+
H^...
...{\frac{1+\alpha}{2}}+xH^{1/2}XK^{1/2}\vert\vert\vert
\quad (\alpha \in [0,1] \ $](img6.gif)
and
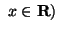
are reported.
- 1
- T. Ando,
Matrix Young inequalities,
Oper. Theory Adv. Appl., 75 (1995), 33-38.
- 2
- R. Bhatia and C. Davis,
More matrix forms of the arithmetic geometric mean inequality,
SIAM J. Matrix Anal. Appl., 14 (1993), 132-136.
- 3
- R. Bhatia and K. R. Parthasarathy,
Positive definite functions and operator inequalities,
Bull. London Math. Soc., 32 (2000), No 2, 214-228.
- 4
-
M. Sh. Birman and M. Z. Solomyak,
Stieltjes double operator integrals,
Dokl. Akad. Nauk SSSR, 165 (1965), 1223-1226 (Russian);
Soviet Math. Dokl., 6 (1965), 1567-1571.
- 5
-
U. Haagerup,
On Schur multipliers in
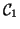 ,
unpublished hand-written notes (1980).
,
unpublished hand-written notes (1980).
- 6
- E. Heinz,
Beiträge zur Störungstheorie der Spektralzerlegung,
Math. Ann., 123 (1951), 415-438.
- 7
- F. Hiai and H. Kosaki,
Comparison of various means for operators,
J. Funct. Anal., 163 (1999), 300-323.
- 8
- F. Hiai and H. Kosaki, Means for matrices and comparison
of their norms,
Indiana Univ. Math. J., 48 (1999), 899-936.
- 9
- F. Hiai and H. Kosaki, Means of Hilbert space operators,
to appear as LNM, Springer.
- 10
- H. Kosaki,
Arithmetic-geometric mean and related inequalities for operators,
J. Funct. Anal., 156 (1998), 429-451.
- 11
- A. McIntosh,
Heinz inequalities and perturbation of spectral families,
Macqaurie Mathematical Reports, 79-0006, 1979.
- 12
-
V. V. Peller,
Hankel operators and differentiability properties of functions
of self-adjoint (unitary) operators,
LOMI Preprints E-1-84, USSR Academy of Sciences Steklov
Mathematical Institute Leningrad Department, 1984.
- 13
- X. Zhan,
Inequalities for unitarily invariant norms,
SIAM J. Matrix Anal. Appl., 20 (1998), 466-470.