|
This is a project on multiscale methods for Coulomb collisions in plasma dynamics, in collaboration with Bruce Cohen and Andris Dimits (LLNL) and with Mark Rosin, Bokai Yann and Lee Ricketson (UCLA). We have worked on several methods:
(1) A hybrid method that represents the velocity distribution function as a kinetic component and a thermal component. The kinetic component is evolved using a binary collision Monte Carlo method. The thermal component is evolved using continuum solver for MHD equations. Interactions between the two component use a thermalization/dethermalization step.
(2) A Milstein method for multidimensional systems, in which the Levy areas are computed using stored approximate values.
(3) A new method for solving the continuum equations for a planar diode, using characteristic variables.
|
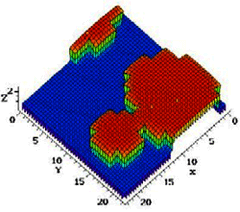
We have developed island dynamics model with a level set simulation method for epitaxial growth, in collaboration with Christian Ratsch and Stan Osher (Math, UCLA), Mark Gyure (HRL Labs), Dimitri Vvedensky (Physics, Imperial), and Andrew Zangwill (Physics, GaTech).
In order to improve epitaxial growth of a III-V semiconductor system, we have developed model
reduction and feedback control for epitaxial growth and for quantum systems, in collaboration with Mark Gyure and
Jenna Zinck (HRL Labs) and Robert Kosut (SCSolutions).
|
 |
|
| |
We are developing a new approach to strain modeling for epitaxial systems. Our model includes atomistic interactions, but is consistent with continuum elasticity. Using this model, we are investigating the effects of strain on growth and structure. This project is in collaboration with Mark Gyure (HRL Labs) and Dimitri
Vvedensky (Physics, Imperial).
|
|
We are simulating the electronic wave function for a layered semiconductor system that includes quantum wells, wires and dots. This system is intended to define a qubit for a quantum communication or computating application. This project is in collaboration with Chris Anderson (Math, UCLA), Ed Croke and Mark Gyure (HRL Labs), and Eli Yablanovitch (EE, UCLA).
|
We have developed a hybrid method, combining particle dynamics and continuum mechanics, for molecular collisions in rarefied gas dynamics, in joint work with Lorenzo Pareschi (U. Ferrarra).
|
The possibility of singularity formation in three-dimensional, incompressible, inviscid fluid flow is a major open problem of mathematical fluid mechanics. Such singularities, if they exist, could be an essential ingredient in turbulent energy dissipation. Our approach to this problem is through computation of singularities in the complex spatial domain. This project is a collaboration with Michael Siegel (NJIT).
|
Microscale needles and other shapes can be fabricated through electrodeposition, in a new process developed by Jack Judy and his group (EE, UCLA). In collaboration with them, we have developed numerical methods for both direct simulation of this electrodeposition and solution of the inverse problem to determine the metal domain layout required to produce a desired shape.
|
 |
|