Location: Mathematical Sciences building, MS 6627
Speakers:
Schedule (tentative):
Saturday, Oct 15
8:00-9:00 Breakfast
9:00-10:00 Antoine Mellet, U. Maryland: A higher order free boundary problem for hydraulic fractures
We will discuss the properties of a free boundary problem which has been proposed to model the propagation of hydraulic fractures. The problem involves a third order non-local parabolic equation which can be seen as an interpolation between the porous media equation and the thin film equation. We will discuss the well-posedness of the problem and prove the existence of self similar solutions.
10:30-11:30 Juhi Jang, USC: Dynamics of expanding gas
I will present a necessary condition for global-in-time existence of smooth compressible inviscid gas/fluid flows and give an example of the solutions to Euler equations satisfying such a condition, which were recently constructed by Sideris. Such solutions are compactly supposed, satisfy the physical vacuum condition, and expand into the vacuum. Global-in-time stability of such solutions will be discussed. This is based on joint work with Mahir Hadzic.
11:30-1:00 Lunch
1:00-2:00 Ben Krause, UBC: Weak (1,1) Bounds for Maximally Truncated Oscillatory Singular Integrals
For any polynomial P(y), and any Calder\'{o}n-Zygmund kernel, K, the maximally truncated osciallatory singular integral below maps L^1 to weak L^1.
\sup_{\epsilon >0} |\int_{|y| > \epsilon} f (x-y) e ^{2 \pi i P (y) } K(y) dy |.
The bound is only a function of the degree of the polynomial P, the dimension, and on the kernel K. The same bound, without maximal truncations, is a special case of a result due to Chanillo and Christ (1987). This is joint work with Michael Lacey.
2:30-3:30 Andrej Zlatos, UCSD: On stochastic homogenization of reaction-diffusion equations
We study spreading of reactions in random media and prove that homogenization takes place under suitable hypotheses. That is, the medium becomes effectively homogeneous in the large-scale limit of the dynamics of solutions. Hypotheses which guarantee this include fairly general stationary ergodic KPP reactions, as well as homogeneous ignition reactions in up to three dimensions perturbed by radially symmetric "impurities" distributed according to a Poisson point process. In contrast with the original (second order) reaction-diffusion equations, the limiting "homogenized" PDE for this model are (first-order) Hamilton-Jacobi equations, and the limiting solutions are discontinuous functions which solve these in a weak sense.
3:30-4:00 Tea
There will be informal groups going out to dinner on Saturday evening (see below).
Sunday, Oct 16
8:00-8:30 Breakfast
8:30-9:30 Wilfrid Gangbo, UCLA: Open problems in Mean Field Games theory
We present some of the recent results in Mean Field Games theory, especially the so–called master equation, the backbone of the MFG theory. Despite the fact that the master equation is a non–local first order equation, we show how it is linked to metric viscosity solutions of a local Hamilton–Jacobi equation on the set of probability measures. (This talk is based on a joint work with A. Swiech).
9:45-10:45 Zaher Hani, Georgia Tech: Non-equilibrium dynamics and statistics for the nonlinear Schrodinger equation
We will start by broadly discussing the problem of non-equilibrium behavior for nonlinear dispersive PDE. This is the characteristic feature of the long-time dynamics of such equations on bounded (possibly very large) domains. One can address this problem from a dynamical perspective and from a statistical physics one. The first tries to construct explicit solutions exhibiting non-equilibrium dynamics, whereas the second tries to derive effective equations for some macroscopic quantities by taking various limits of the original system. We shall compare and discuss some recent developments on both perspectives for the nonlinear Schrodinger equation.
11:15-12:15 Monica Visan, UCLA: Symplectic non-squeezing for the cubic NLS on the plane
We prove that the flow of the cubic NLS in two dimensions cannot squeeze a ball in $L^2$ into a cylinder of lesser radius. This is a PDE analogue of Gromov's non-squeezing theorem for an infinite-dimensional Hamiltonian PDE in infinite volume. It is joint work with R. Killip and X. Zhang.
There will be an informal (free) registration during the conference.
A list of hotels near UCLA can be found here. A campus map can be found here.
Thanks to NSF grant DMS-1603385, we now have some funds to support graduate student travel to attend this conference. Please contact tao@math.ucla.edu for details on this (or for any other inquiries). Reimbursement forms will be provided at the conference.
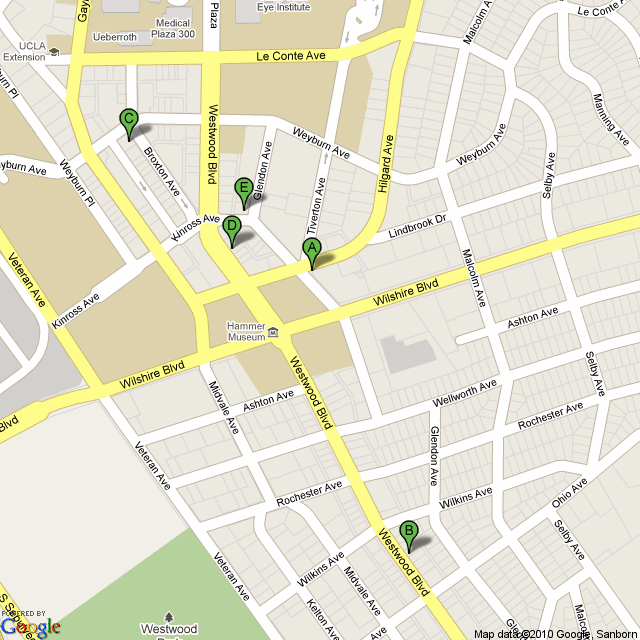
To get to campus, consult this Google map, centered on the Westwood Blvd parking booth.
Here is a map to help with on-campus navigation:
Key:
X = Location of lectures: Math Sciences building, room 6627.
P = Parking: (1) Parking booth on Westwood Plaza (=Blvd). (2) Self-service parking entrance to structure #2.
F = On-campus food: Kerckhoff coffee house (salads/sandwiches) and Ackerman Union (Sbarro/Panda Express/Carls Jr./Rubio's)
There are numerous eateries in Westwood village and further down Westwood Blvd. Here is a selection:
A = Palomino Very nice, but a little pricey.
B = Flame Persian Cuisine One of several Persian restaurants; this neighbourhood is known as "Little Persia".
C = California Pizza Kitchen Pizza.
D = Noodle World Very economical. (closed)
E = Westwood Brewing Co It's a bar. (closed)
Local organisers: John Garnett, Michael Hitrik, Inwon Kim, Terence Tao
Global organisers: Ioan Bejenaru, Jacob Sterbenz
Previous SCAPDE meetings: