Week 4 Discussion Notes

Table of Contents

• Change of Variables

Change of Variables

We're already familiar with some change of variables: polar coordinates, where $x = r\cos\theta$, $y = r\sin\theta$. When integrating, this gives us

In general, coordinate changes are of the form

In other words, $G$ changes coordinates from $\p{u, v}$ to $\p{x, y}$. With this notation, we get the formula for integration:

where

In the matrix above, the first column is all the $u$-derivatives, and the second column is all the $v$-derivatives.

To help you remember this, you should hopefully remember $u$-substitution in 1D:

Copying this, we get something like this:

But instead of $G'\p{u, v}$, we put the Jacobian (in absolute values) there instead.

Example 1.

With polar coordinates $\p{x, y} = \p{r\cos\theta, r\sin\theta}$,

$$\Jac{G} = \det \begin{pmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & \phantom{-}r\cos\theta \end{pmatrix} = r\cos^2\theta + r\sin^2\theta = r,$$

so

$$\diff{x} \,\diff{y} = r \,\diff{r} \,\diff\theta,$$

which is exactly what we expect.

Example 2.

Find a change of variables to evaluate $\displaystyle \iint_{\mathscr{R}} \p{x + y}^2 e^{x^2-y^2} \,\diff{x} \,\diff{y}$, where $\mathscr{R}$ is the square with vertices $\p{1, 0}, \p{0, 1}, \p{-1, 0}, \p{0, -1}$.

Solution.

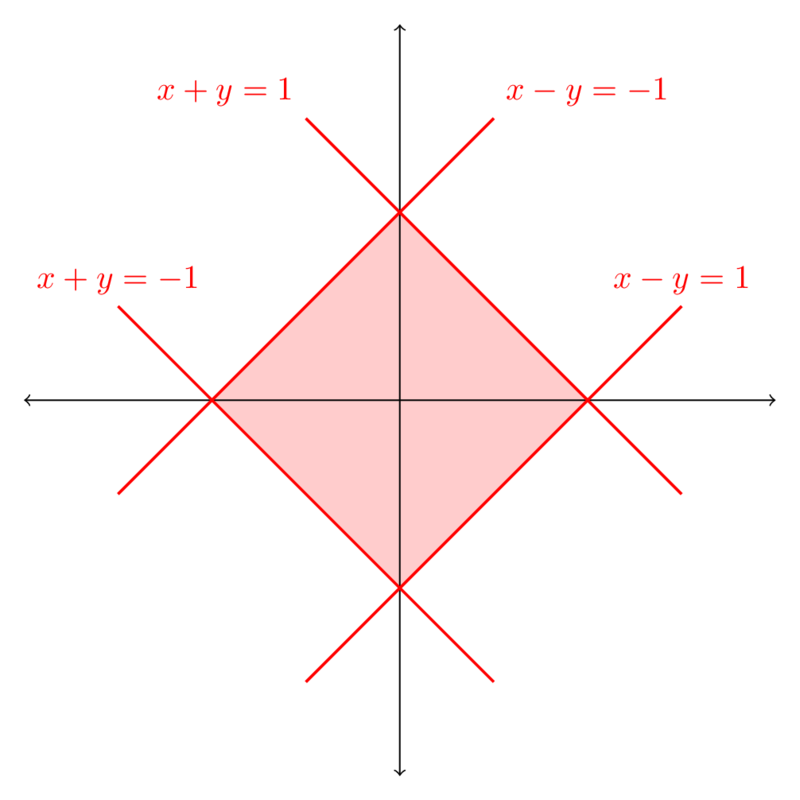
We can express the region $\mathscr{R}$ via

$$\mathscr{R} = \left\{ \begin{gathered} -1 \leq x + y \leq 1, \\ -1 \leq x - y \leq 1 \end{gathered} \right\}.$$

This suggests that we let $u = x + y$ and $v = x - y$ because the region is a lot easier to express in these coordinates:

$$\mathscr{R} = \left\{ \begin{gathered} -1 \leq u \leq 1 \\ -1 \leq v \leq 1 \end{gathered} \right\}.$$

Solving for $x$ and $y$, we get

$$\p{x, y} = \p{\frac{u + v}{2}, \frac{u - v}{2}},$$

so the Jacobian is

$$\Jac{G} = \det \begin{pmatrix} \dfrac{1}{2} & \phantom{-}\dfrac{1}{2} \\[2ex] \dfrac{1}{2} & -\dfrac{1}{2} \end{pmatrix} = -\frac{1}{2}.$$

(I switched $u$ and $v$, so this is a little different from what's on the recording.)

Thus,

$$\diff{x} \,\diff{y} = \abs{\Jac{G}} \,\diff{u} \,\diff{v} = \frac{1}{2} \,\diff{u} \,\diff{v}.$$

Applying the change of variables to the integral,

$$\begin{aligned} \iint_{\mathscr{R}} \p{x + y}^2 e^{x^2-y^2} \,\diff{x} \,\diff{y} &= \frac{1}{2} \int_{-1}^1 \int_{-1}^1 u^2 e^{uv} \,\diff{u} \,\diff{v} \\ &= \boxed{\frac{2}{e}}. \end{aligned}$$