<Home>Teaching><MATH 131B (Winter 2022)>Week 7 Discussion Notes

Week 7 Discussion Notes

Uniform Convergence

Uniform Convergence

There's not too much to say about this section in the book since a lot of my examples have been related to this concept, and most of the properties about uniform convergence of functions $\func{f_n}{\R}{\R}$ hold for more general functions $\func{f_n}{\p{X, d_X}}{\p{Y, d_Y}}$ . For example, if $\set{f_n}_n$ is a sequence of continuous functions that converges uniformly to a function $f$ , then $f$ is also continuous.

A lot of the examples we did were on the space $C\p{\br{0, 1}}$ , i.e., the metric space of continuous functions on $\br{0, 1}$ with the $\sup$ -metric. However, the general definitions are slightly different:

Definition

Let $\p{X, d_X}$ and $\p{Y, d_Y}$ be metric spaces. We define

\begin{aligned} B\p{X, Y} &= \set{\func{f}{X}{Y} \st f \text{ is bounded}} \\ C_b\p{X, Y} &= \set{\func{f}{X}{Y} \st f \text{ is bounded and continuous}}. \end{aligned}

When equipped with the $\sup$ -metric, i.e.,

d\p{f, g} = \sup_{x \in X}{\abs{f\p{x} - g\p{x}}},

these function spaces are metric spaces.

Remark.

The key difference here is the additional assumption that our functions are bounded. In our example $C\p{\br{0, 1}}$ , we're using $X = \br{0, 1}$ , which is compact. Thus, continuous functions are automatically bounded, so we didn't need to include it in the definition.

Boundedness is important for our metric to make sense. For example, if $X = Y = \R$ and $f\p{x} = x^2$ , then

d\p{f, 0} = \sup_{x \in \R}{\abs{x^2 - 0}} = \infty.

The main result is the following theorem:

Theorem

Let $\p{X, d_X}$ be a metric space, and let $\p{Y, d_Y}$ be a complete metric space. Then $B\p{X, Y}$ and $C_b\p{X, Y}$ are complete.

Remark.

Note that it's important that $Y$ is a complete metric space. In the proof, we use it to find a pointwise limit of a Cauchy (with respect to the $\sup$ -metric) sequence.

Dini's Theorem

In general, uniform convergence implies pointwise convergence, but the converse is not true, i.e., there are sequences which converge pointwise but not uniformly. In some very special cases, though, we can upgrade pointwise convergence to uniform convergence:

Theorem (Dini)

Let $\p{X, d_X}$ and $\p{Y, d_Y}$ be metric spaces, and let $\func{f_n, f}{X}{\R}$ be functions. Assume that:

$X$ is compact
$f, f_n$ are continuous for all $n$
$f_n\p{x} \to f\p{x}$ for all $x \in X$
$f_{n+1} \leq f_n$ for all $n$

Then $f_n \to f$ uniformly.

This type of result is very rare, which I'll demonstrate by showing that in general, you can't remove any of the assumptions:

Compactness is essential:

Example 1.

Let $X = \R$ (which is unbounded, so not compact) and let $\func{f_n}{\R}{\R}$ be the following function:

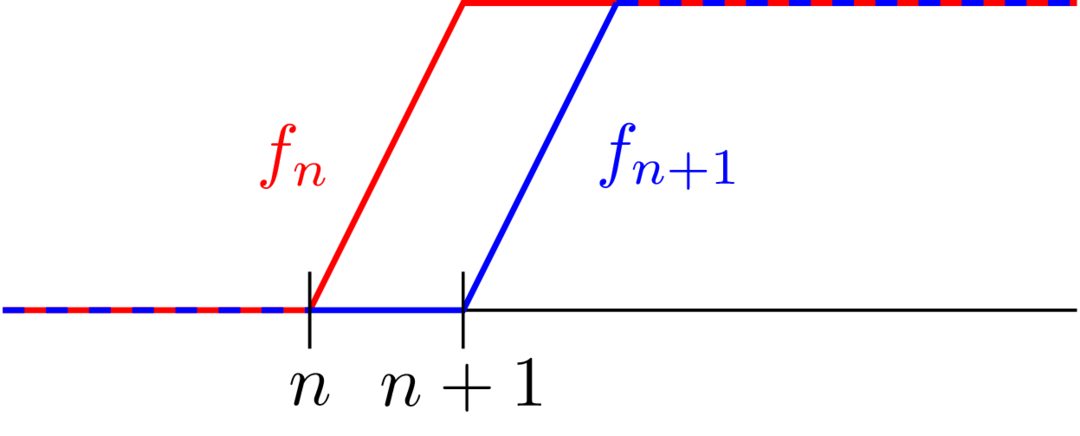
In words, $f_n\p{x} = 0$ for $x \leq n$ , $f_n\p{x} = 1$ for $x \geq n+1$ , and it's linear on $n \leq x \leq n+1$ . From the picture, it's clear that $f_n$ is continuous for all $n$ and that $f_{n+1} \leq f_n$ (the blue function always sits below the red function).

In this example, $f_n$ converges pointwise to $0$ . To see this, let $x \in \R$ . Then there exists $n_0 \in \N$ such that $x \leq N$ , so if $n \geq N$ , then $f_n\p{x} = 0$ . Thus, $f\p{x} = 0$ , which is also continuous. However, this convergence is not uniform:

\sup_{x \in \R}{\abs{f_n\p{x} - 0}} = 1.

Continuity of $f$ is essential:

Example 2.

We've seen this example before: $X = \br{0, 1}$ and $f_n\p{x} = x^n$ . Then $X$ is compact, $f_n$ is continuous for all $n$ , and $f_n \to f$ pointwise, where

f\p{x} = \begin{cases} 0 & \text{if } 0 \leq x < 1, \\ 1 & \text{if } x = 1. \end{cases}

However, $f$ is not continuous, and there's no chance $f_n \to f$ uniformly, since that would imply that $f$ is continuous.

Monotonicity in $n$ is essential:

Example 3.

Let $X = \br{0, 1}$ and let $f_n$ be the following function:

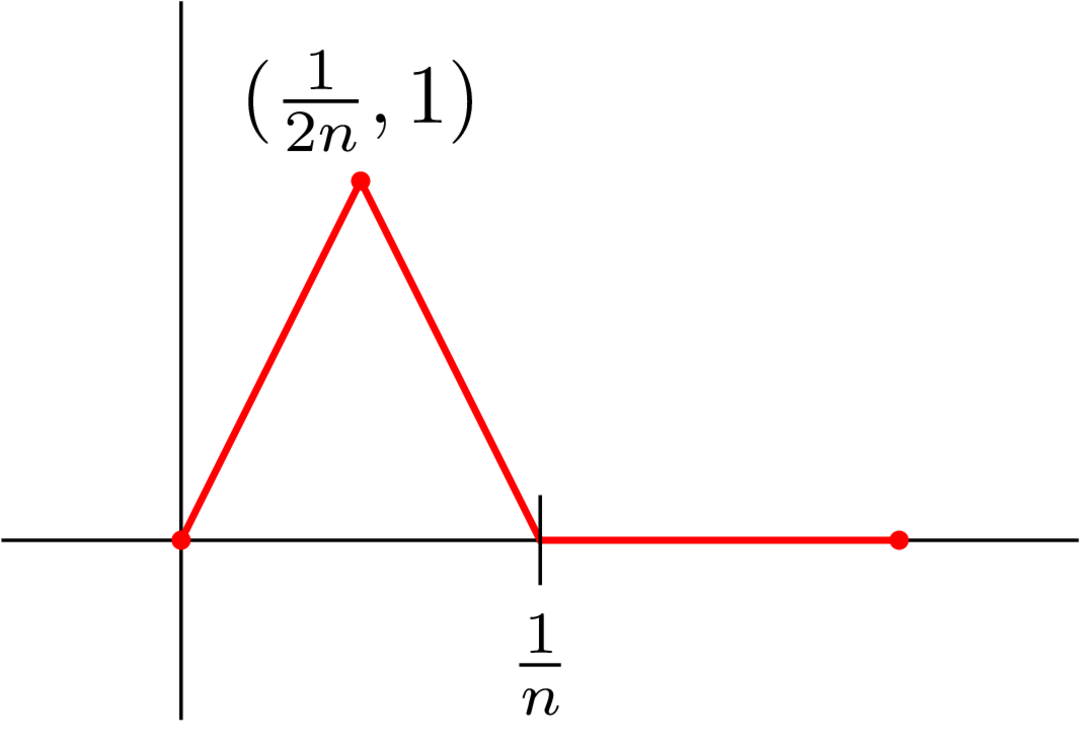
$X$ is compact as before, $f_n$ is continuous for all $n$ , and $f_n \to 0$ pointwise: notice that if $x = 0$ , then $f_n\p{0} = 0$ for all $n \geq 1$ , and if $x > 0$ , then there exists $N \in \N$ such that $0 < \frac{1}{N} < x$ . Thus, if $n \geq N$ , then $f_n\p{x} = 0$ also. However,

\sup_{x \in \br{0,1}}{\abs{f_n\p{x} - 0}} = 1,

so this convergence is not uniform.

Differentiation and Uniform Convergence

Example 4.

True or false: If $f_n$ is a sequence of differentiable functions on $\br{-1, 1}$ and $f_n \to f$ uniformly, then $f$ is differentiable.

Solution.

This is false. Let $f_n$ be the following function:

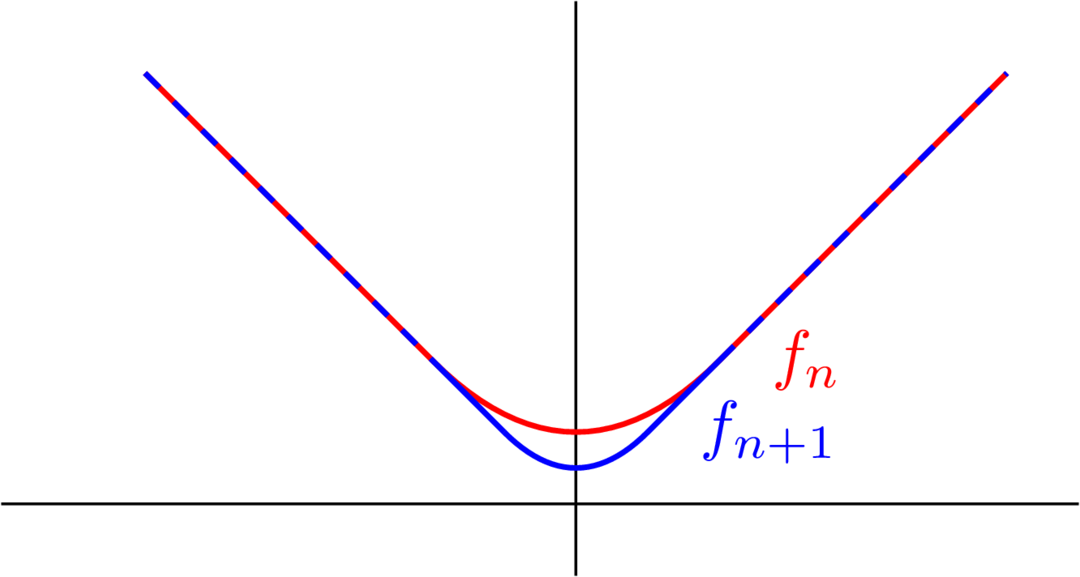
In words, $f_n$ is a straight line outside the interval $\br{-\frac{1}{n}, \frac{1}{n}}$ , and on this interval, it's equal to a parabola (stretched accordingly) that makes $f_n$ differentiable on the whole interval with minimum value $\frac{1}{2n}$ at the origin.

$f_n$ converges to $\abs{x}$ pointwise, and in fact, this convergence is uniform since the maximum distance is attained at the origin. However, while $f_n$ is differentiable, $\abs{x}$ is not differentiable at the origin.

Example 5.

True or false: If $f_n$ is a sequence of differentiable functions on $\br{-1, 1}$ and $f_n \to f$ uniformly, then $f$ is differentiable at at least one point.

Solution.

This is also false. The Weierstrass function is the uniform limit of differentiable functions (in fact, these functions are differentiable infinitely many times), but is differentiable nowhere.

Integration and Uniform Convergence

Example 6.

True or false: If $\func{f_n}{\R}{\R}$ is a sequence of functions that converges uniformly to a function $f$ , then $\int f_n\p{x} \,\diff{x} \to \int f\p{x} \,\diff{x}$ .

Solution.

This is (a little surprisingly) false. One example is $f_n\p{x} = \frac{1}{n}$ , which converges uniformly to $0$ , but

\int f_n\p{x} \,\diff{x} = \infty,

which definitely doesn't converge to $0$ .

A more interesting example (i.e., one where $\int f_n\p{x} \,\diff{x}$ is finite for every $n$ ) is the following:

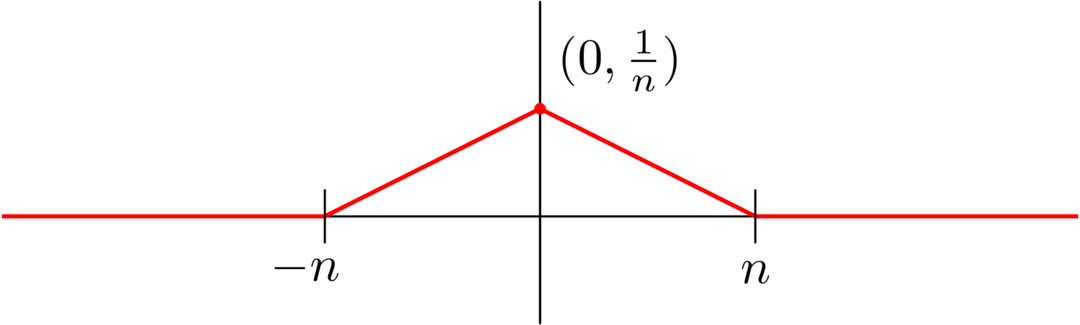
Like the above, $f_n \to 0$ uniformly since the maximum distance is $\frac{1}{n}$ for any $n$ . However,

\int_{-n}^n f_n\p{x} \,\diff{x} = \frac{1}{n} \cdot n = 1,

which doesn't converge to $0$ .

Example 7.

True or false: If $\func{f_n}{\br{0, 1}}{\R}$ is a sequence of functions that converges uniformly to a function $f$ , then $\int f_n\p{x} \,\diff{x} \to \int f\p{x} \,\diff{x}$ .

Solution.

This one is true. The key difference between this situation and the previous situation is that we're now working on an interval with finite length. To prove it, let $\epsilon > 0$ . By uniform convergence, there exists $N \in \N$ such that if $n \geq N$ , then

\sup_{x \in \br{0, 1}}{\abs{f_n\p{x} - f\p{x}}} < \epsilon.

Thus, if $n \geq N$ ,

\begin{aligned} \abs{\int_0^1 f_n\p{x} \,\diff{x} - \int_0^1 f\p{x} \,\diff{x}} &= \abs{\int_0^1 f_n\p{x} - f\p{x} \,\diff{x}} \\ &\leq \int_0^1 \abs{f_n\p{x} - f\p{x}} \,\diff{x} \\ &\leq \int_0^1 \sup_{y \in \br{0,1}}{\abs{f_n\p{y} - f\p{y}}} \,\diff{x} \\ &\leq \int_0^1 \epsilon \,\diff{x} \\ &= \epsilon. \end{aligned}

Week 7 Discussion Notes

Table of Contents

Uniform Convergence

Definition

Remark.

Theorem

Remark.

Dini's Theorem

Theorem (Dini)

Example 1.

Example 2.

Example 3.

Differentiation and Uniform Convergence

Example 4.

Solution.

Example 5.

Solution.

Integration and Uniform Convergence

Example 6.

Solution.

Example 7.

Solution.