<Home>Teaching><MATH 131A (Winter 2021)>Week 4 Discussion Notes

Week 4 Discussion Notes

Table of Contents

Supremums and Infimums

Definition

Let S⊆RS \subseteq \R be a non-empty set. If there exists x∈Sx \in S such that s≤xs \leq x for all s∈Ss \in S, then we call xx the maximum of SS and we write x=max⁡Sx = \max{S}.
Exercise 1.

Define min⁡S\min{S}.

At first glance, max⁡S\max{S} and sup⁡S\sup{S} look like the same thing. However, there's a key difference: max⁡S\max{S} has to be an element of SS, but sup⁡S\sup{S} doesn't have to be.

Example 1.

If S=[0,1)S = \pco{0, 1}, then SS has no maximum, but sup⁡S=1\sup{S} = 1.

On the other hand, if S=[0,1]S = \br{0, 1}, then max⁡S=sup⁡S=1\max{S} = \sup{S} = 1.
Example 2.

(4.8) Let SS and TT be non-empty subsets of R\R such that s≤ts \leq t for all s∈Ss \in S and t∈Tt \in T.

  1. Observe that SS is bounded above and TT is bounded below.
  2. Prove sup⁡S≤inf⁡T\sup{S} \leq \inf{T}.
Solution.
  1. Any element of TT is an upper bound of SS, and any element of SS is a lower bound of TT.
  2. If t∈Tt \in T, then tt is an upper bound for SS, so by definition, sup⁡S≤t\sup{S} \leq t. This means that sup⁡S\sup{S} is a lower bound for TT, so sup⁡S≤inf⁡T\sup{S} \leq \inf{T}.

Density of Q\Q in R\R

Theorem

For any a,b∈Ra, b \in R with a<ba < b, there exists a rational q∈Qq \in \Q such that q∈(a,b)q \in \p{a, b}.

We know that Q\Q has gaps in it, which is why we work with R\R. However, the fact that Q\Q is dense means that the gaps are very "tiny". In other words, no matter how far you zoom in, you'll always see infinitely many rational numbers.

Example 3.

(4.11) Consider a,b∈Ra, b \in \R where a<ba < b. Show that there are infinitely many rationals between aa and bb.
Solution.

(Hint) You can use induction with the following statement to prove this: "there are at least nn rationals in (a,b)\p{a, b}" for all n∈Nn \in \N. You could also do this by contradiction—either is fine.

Sequences

Definition

A sequence is a function s ⁣:N→R\func{s}{\N}{\R}, where we write sn=s(n)s_n = s\p{n} and {sn}n={sn∣n∈N}\set{s_n}_n = \set{s_n \mid n \in \N}.

If there exists L∈RL \in \R such that:

For all ε>0\epsilon > 0, there exists N∈RN \in \R such that ∣sn−L∣<ε\abs{s_n - L} < \epsilon for all N>NN > N,

we say that sns_n converges to LL and we write lim⁡n→∞=L\displaystyle \lim_{n\to\infty} = L. Otherwise, if no such LL exists, then we say that sns_n is divergent.

Intuitively, the limit of a sequence is what it gets "really close to" as nn "gets really big". To make this more precise, we need to quantify two things:

  • "really close to" (this is ε\epsilon)
  • "gets really big" (this is NN)

With this interpretation, you can read the definition like this:

If nn is large enough, we can make ∣sn−L∣\abs{s_n - L} as small as we want.

The definition is (somewhat) intuitive, but using the definition to prove things is generally pretty tricky.

Example 4.

(Similar to 8.1(c)) Prove lim⁡n→∞4n+37n−5=47\displaystyle \lim_{n\to\infty} \frac{4n+3}{7n-5} = \frac{4}{7}.
Solution.

When proving limits, we're given an ε>0\epsilon > 0 (something out of your control), and we need to find NN (something you can control). The general strategy is to work backwards: start with

∣4n+37n−5−47∣=∣21+207(7n−5)∣=417(7n−5)\abs{\frac{4n+3}{7n-5} - \frac{4}{7}} = \abs{\frac{21 + 20}{7\p{7n-5}}} = \frac{41}{7\p{7n-5}}

when n≥1n \geq 1. In the end, we want to make this quantity smaller than ε\epsilon, so it's okay to look at bigger quantities. If we make the denominator smaller, then we get something bigger:

∣417(7n−5)∣≤417(7n−5n)=4114n.\abs{\frac{41}{7\p{7n-5}}} \leq \frac{41}{7\p{7n - 5n}} = \frac{41}{14n}.

If we can make 4114n<ε\frac{41}{14n} < \epsilon, then we're done. We're in good shape because we can:

4114n<ε  ⟺  n>4114ε.\frac{41}{14n} < \epsilon \iff n > \frac{41}{14\epsilon}.

None of what I wrote above is a proof (though it almost looks like one); it's just scratch work that I used to figure out what NN needs to be. Given an ε>0\epsilon > 0, our candidate for NN is 4114ε\frac{41}{14\epsilon}, and it's now time to verify that this works. The following is the beginning of the proof of the limit:

Let ε>0\epsilon > 0. If we set N=4114εN = \frac{41}{14\epsilon}, then if n>Nn > N,

∣sn−L∣=∣4n+37n−5−47∣=417(7n−5)≤4114n<4114N=4114(41/14ε)=ε.\begin{aligned} \abs{s_n - L} = \abs{\frac{4n+3}{7n-5} - \frac{4}{7}} = \frac{41}{7\p{7n-5}} &\leq \frac{41}{14n} \\ &< \frac{41}{14N} \\ &= \frac{41}{14\p{41/14\epsilon}} \\ &= \epsilon. \end{aligned}

ε\epsilon was arbitrary, so what we wrote works for any ε\epsilon, which completes the proof.
Example 5.

(Similar to 8.1(d)) Prove lim⁡n→∞n+3n2−3=0\displaystyle \lim_{n\to\infty} \frac{n+3}{n^2-3} = 0.
Solution.

We're going to apply the same strategy and work backwards: if n>2n > 2, then

∣n+3n2−3∣=n+3n2−3≤n+3n2−9=n+3(n+3)(n−3)=1n−3.\abs{\frac{n + 3}{n^2 - 3}} = \frac{n + 3}{n^2 - 3} \leq \frac{n + 3}{n^2 - 9} = \frac{n + 3}{\p{n + 3}\p{n - 3}} = \frac{1}{n - 3}.

Like before, if we can make 1n−3<ε\frac{1}{n - 3} < \epsilon, then that gives us our candidate for NN:

1n−3<ε  ⟺  n>3+1ε.\frac{1}{n - 3} < \epsilon \iff n > 3 + \frac{1}{\epsilon}.

So N=3+1εN = 3 + \frac{1}{\epsilon} should work. We just need to prove that this works:

Let ε>0\epsilon > 0. If N=3+1εN = 3 + \frac{1}{\epsilon}, then for n>Nn > N, we get

∣sn−L∣=∣n+3n2−3∣=n+3n2−3≤n+3n2−9=1n−3<1N−3=13+1ε−3=ε.\begin{aligned} \abs{s_n - L} = \abs{\frac{n + 3}{n^2 - 3}} = \frac{n + 3}{n^2 - 3} &\leq \frac{n + 3}{n^2 - 9} \\ &= \frac{1}{n - 3} \\ &< \frac{1}{N - 3} \\ &= \frac{1}{3 + \frac{1}{\epsilon} - 3} \\ &= \epsilon. \end{aligned}

To summarize, this is the basic strategy for proving limits through the definition:

  1. Work backwards and use inequalities figure out a candidate for NN.
    • Generally, you want to make the numerator bigger (in absolute value) and/or the denominator smaller (in absolute value).
  2. Write out the proof with your candidate of NN.
    • If you set it up right, then your proof will just look like what you wrote in step 1, but in reverse.

The definition can also be used to prove some useful facts about limits.

Proposition

Let {sn}n\set{s_n}_n be a sequence. Suppose sn>0s_n > 0 for all n≥1n \geq 1 and that L=lim⁡n→∞snL = \displaystyle\lim_{n\to\infty} s_n exists. Then L≥0L \geq 0.
Proof.

Intuitively, it's obvious. However, proving it is a bit tricky since we need to use the definition of a limit. We'll do this by contradiction: assume for the sake of contradiction that L<0L < 0. We then have the following picture:

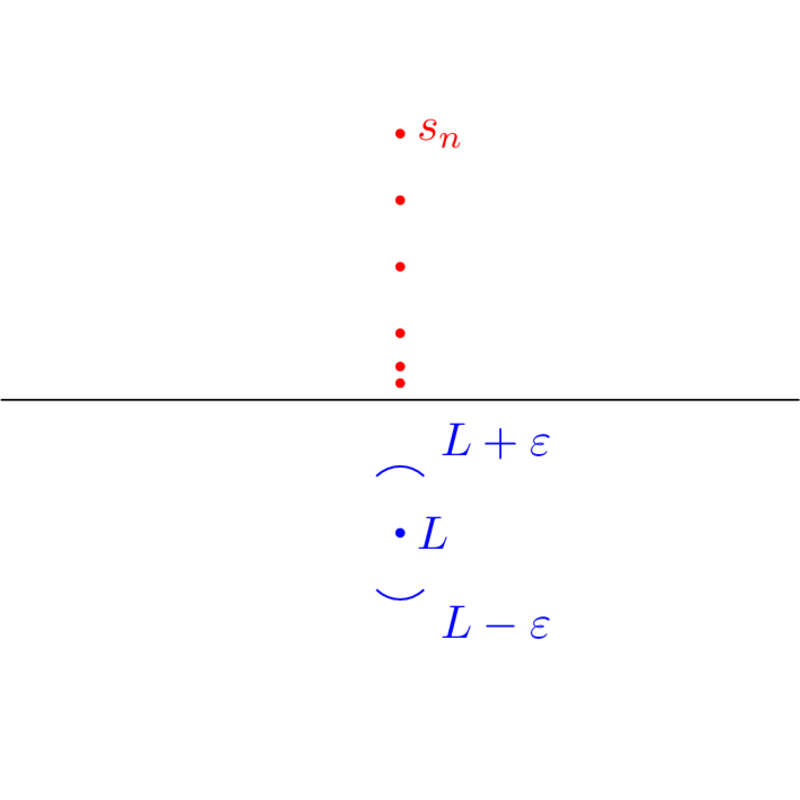
The definition of a limit tells you that for any ε>0\epsilon > 0, eventually all the points in your sequence lie in the interval (L−ε,L+ε)\p{L - \epsilon, L + \epsilon}. From the picture, you should be able to see why that's impossible: if ε\epsilon is small enough, then that implies that the sequence is eventually negative, which is a contradiction. Now we need to write that down:

If ε\epsilon is too large, then we won't get a contradiction. Thus, we need to be smart about how we pick it. Based on the picture, if we let ε\epsilon be half the distance from LL to 00, then we should be able to get a contradiction, i.e., let ε=∣L∣2=−L2>0\epsilon = \frac{\abs{L}}{2} = -\frac{L}{2} > 0. By definition of the limit, there exists N∈RN \in \R such that if n>Nn > N, then ∣sn−L∣<ε\abs{s_n - L} < \epsilon. But this means

−ε<sn−L<ε  ⟹  sn<L+ε=L−L2=L2<0,-\epsilon < s_n - L < \epsilon \implies s_n < L + \epsilon = L - \frac{L}{2} = \frac{L}{2} < 0,

which is impossible, so L≥0L \geq 0 to begin with. □\square
Remark.

Notice that even though sns_n is strictly positive for all nn, its limit can still be equal to 00. For example, sn=1ns_n = \frac{1}{n} has limit 00 even though all of its terms are 00.