<Home>Teaching><MATH 131A (Winter 2021)>Week 3 Discussion Notes

Week 3 Discussion Notes

Induction
Rational Numbers $\Q$
Real Numbers $\R$
- Definition
- The Least Upper Bound Property

Induction

Example 1.

Prove $1^3 + 2^3 + \cdots + n^3 = \p{1 + 2 + \cdots + n}^2$ for all positive integers $n$ .

Solution.

Base case: ( $n = 1$ ) Plugging $n = 1$ into the left side, we get

1^3 = 1 = 1^2,

so the base case holds.

Inductive step: Suppose the equation is true for $n = k$ , i.e., assume that

1^3 + 2^3 + \cdots + k^3 = \p{1 + 2 + \cdots + k}^2

is true. We need to show that it's true for $n = k + 1$ :

\begin{aligned} \p{1 + 2 + \cdots + k + \p{k + 1}}^2 &= \p{\p{1 + 2 + \cdots + k} + \p{k + 1}}^2 \\ &= \p{1 + 2 + \cdots + k}^2 + 2\p{k + 1}\p{1 + 2 + \cdots + k} + \p{k + 1}^2 \\ &= \p{1^3 + 2^3 + \cdots + k^3} + 2\p{k + 1} \cdot \frac{k\p{k + 1}}{2} + \p{k + 1}^2 \\ &= \p{1^3 + 2^3 + \cdots + k^3} + k\p{k + 1}^2 + \p{k + 1}^2 \\ &= \p{1^3 + 2^3 + \cdots + k^3} + \p{k + 1}^2\p{k + 1} \\ &= 1^3 + 2^3 + \cdots + k^3 + \p{k + 1}^3, \end{aligned}

so the inductive step holds. Thus, by induction, the formula is true for all positive integers.

Example 2.

Prove $7^n - 6n - 1$ is divisible by $36$ for all positive integers $n$ .

Solution.

To make things easier to write, I'll be writing $36 \mid k$ to mean " $36$ divides $k$ ".

Base case: ( $n = 1$ ) When $n = 1$ , we get

7^1 - 6 - 1 = 0,

and $36$ divides $0$ , so the base case holds.

Inductive step: Assume $7^k - 6k - 1$ is divisible by $36$ . We need to show that $7^{k+1} - 6\p{k + 1} - 1$ is also divisible by $36$ :

\begin{aligned} 7^{k+1} - 6\p{k + 1} - 1 &= 7 \cdot 7^k - 6k - 6 - 1 \\ &= \p{6 + 1} \cdot 7^k - 6k - 6 - 1 \\ &= 6 \cdot 7^k - 6 + \p{7^k - 6k - 1} \\ &= 6 \cdot \p{7^k - 1} + \p{7^k - 6k - 1}. \end{aligned}

Since $36 \mid \p{7^k - 6k - 1}$ , there exists $m \in \Z$ such that $7^k - 6k - 1 = 36m$ . Rearranging, this also tells us that $7^k - 1 = 36m + 6k$ , so

\begin{aligned} 7^{k+1} - 6\p{k + 1} - 1 &= 6 \cdot \p{7^k - 1} + \p{7^k - 6k - 1} \\ &= 6 \cdot \p{36m + 6k} + 36m \\ &= 36 \cdot \p{6m + 1} + 36m, \end{aligned}

which means $36 \mid \p{7^{k+1} - 6\p{k + 1} - 1}$ . By induction, this is true for all positive integers.

Rational Numbers $\Q$

Theorem (rational roots theorem)

Consider the equation

c_n x^n + c_{n-1} x^{n-1} + \cdots + c_0 = 0,

where $c_0, c_1, \ldots, c_n \in \Z$ . Let $r = \frac{c}{d}$ be a rational solution to the equation, where $r$ is simplified so that $c$ and $d$ have no factors in common. Then $c$ is a factor of $c_0$ and $d$ is a factor of $c_n$ .

The intuition for the proof is as follows: $\frac{c}{d}$ is a root of $dx - c$ , so we want to factor the polynomial into

\begin{aligned} c_n x^n + c_{n-1} x^{n-1} + \cdots + c_0 &= \p{dx - c}\p{a_{n-1}x^{n-1} + \cdots + a_0} \\ &= da_{n-1} x^n + \cdots - ca_0. \end{aligned}

If we compare coefficients, we see $c_n = da_{n-1}$ and $-ca_0 = c_0$ , so if $a_{n-1}$ and $a_0$ are integers, then $d$ should divide $c_n$ and $c$ should divide $c_0$ . We can't guarantee that $a_{n-1}$ and $a_0$ are integers, though, so this isn't a proof.

Corollary

If $p$ is a prime and $n \geq 2$ is a positive integer, then $\sqrt[n]{p}$ is irrational.

Proof.

(Sketch)

Consider the equation

x^n - p = 0.

Write out all the possible rational solutions and show that none of them are actually solutions. (Recall that $1$ is not a prime.) $\square$

Real Numbers $\R$

Definition

One problem with $\Q$ is that it has lots of gaps. For example, you can "separate" $\Q$ into

\Q = \set{q \in \Q \mid q^2 < 2} \cup \set{q \in \Q \mid q^2 > 2},

i.e., $\Q$ "jumps over" $\sqrt{2}$ . This is why we want to work with the real numbers; it has no gaps.

Definition (the real numbers)

The real numbers, denoted $\R$ , is the ordered field with the least upper bound property.

In other words, $\R$ is what you "expect it to be":

Ordered means you can compare two numbers, i.e., they're equal or one is bigger than the other.
Field means you can add, subtract, multiply, and divide like you always did.

The least upper bound property takes a bit more work to understand.

The Least Upper Bound Property

Definition

Let $S \subseteq \R$ . Then

$S$ is bounded above if there exists $B \in \R$ such that $\forall x \in S$ , $x \leq B$ . We call $B$ an upper bound for $S$ .
$S$ is bounded below if there exists $L \in \R$ such that $\forall x \in S$ , $L \leq x$ . We call $L$ a lower bound for $S$ .
$S$ is bounded if it is both bounded above and bounded below.

Example 3.

If $a, b$ are finite, then:

$\p{-\infty, b}$ is bounded from above (by $b$ ) but not from below,
$\p{a, \infty}$ is bounded from below (by $a$ ) but not from above,
$\p{a, b}$ is bounded.

Now we can understand what the least upper bound property is:

Definition

$\R$ has the least upper bound property, that is:

If $S \subseteq \R$ is non-empty and bounded above, then there exists $x^* \in \R$ such that:

$x^*$ is an upper bound for $S$ , and
if $B$ is another upper bound for $S$ , then $x^* \leq B$ .

When this happens, we call $x^*$ the supremum of $S$ and write $x^* = \sup{S}$ .

The least upper bound is what it sounds like: it's an upper bound that's smaller than any other upper bound.

Proposition

If $\sup{S}$ exists, then it is unique.

Proof.

Suppose $x, x'$ are two least upper bounds for $S$ .

Since $x$ is a least upper bound and $x'$ is another upper bound for $S$ , we get $x \leq x'$ .
Similarly, $x'$ is a least upper bound and $x$ is an upper bound for $S$ , so $x' \leq x$ .

Putting these together, we get $x = x'$ . $\square$

Example 4.

If $a < b$ and $b$ is finite, then $\sup{\p{a, b}} = b$ . Here, $a$ is allowed to be $-\infty$ .

Solution.

To show that $b$ is the least upper bound, we need to show:

it is an upper bound, and
if $M$ is another upper bound for $\p{a, b}$ , then $b \leq M$ .

By definition, if $x \in \p{a, b}$ , then $a < x < b$ , so $b$ is an upper bound for $\p{a, b}$ , which proves (1).

We'll prove (2) by contradiction: assume that $M$ is another upper bound for $\p{a, b}$ , but $M < b$ . There are two cases:

Case 1: If $a = -\infty$ , then $M \in \p{-\infty, b}$ .

Case 2: If $a$ is finite, then $\frac{a + b}{2} \in \p{a, b}$ . By definition of upper bound, $\frac{a + b}{2} \leq M$ , so

a < \frac{a + b}{2} \leq M < b,

so $M \in \p{a, b}$ .

In either case, $M \in \p{a, b}$ , but this means that $\frac{M + b}{2} \in \p{a, b}$ , so

M < \frac{M + b}{2} < b,

a contradiction. Thus, $b \leq M$ to begin with, which completes the proof.

Definition

We say that $\R$ has the greatest lower bound property if:

Whenever $S \subseteq \R$ is non-empty and bounded below, there exists $x_* \in \R$ such that:

$x_*$ is a lower bound for $S$ , and
if $L$ is another lower bound for $S$ , then $L \leq x_*$ .

In this case, we say $x_*$ is the infimum of $S$ , and we write $x_* = \inf{S}$ .

Proposition

$\R$ has the greatest lower bound property.

Proof.

The closest thing we have to this is the least upper bound property, so we want to try to use it somehow.

The idea is try to reverse engineer what the greatest lower bound for $S$ would be. If we "mirror" $S$ , i.e., consider the set $-S = \set{-x \mid x \in S}$ , then we get something like this:

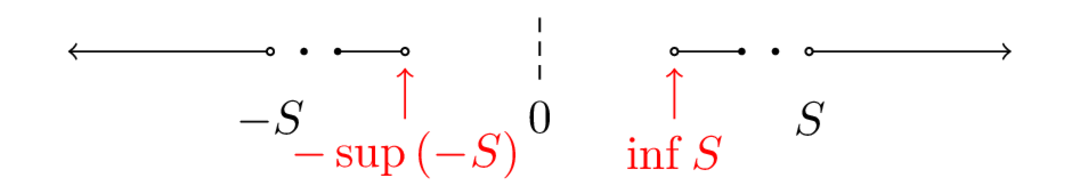
Based on this picture, $\inf{S}$ should correspond to $\sup\,\p{-S}$ after the reflection. Since $S \neq \emptyset$ , this tells us that $-S \neq \emptyset$ also. We also know that $S$ is bounded below, so let $L$ be a lower bound for $S$ . Then given $-x \in S$ ,

L \leq x \implies -x \leq -L,

so $-L$ is an upper bound for $-S$ , i.e., $-S$ is bounded from above. By the least upper bound property, $\sup\,\p{-S}$ exists.

Based on the picture, we will try to prove that $\inf{S} = -\sup\,\p{-S}$ . As before, there are two things to prove:

$-\sup\,\p{-S}$ is a lower bound for $S$ , and
if $L$ is another lower bound for $S$ , then $L \leq -\sup\,\p{-S}$ .

To show (1), let $x \in S$ . Then $-x \in -S$ , so by definition of the supremum,

-x \leq \sup\,\p{-S} \implies -\sup\,\p{-S} \leq x.

Since $x$ was arbitrary, this means $-\sup\,\p{-S}$ is a lower bound for $S$ .

To show (2), let $L$ be another lower bound for $S$ . Then by the same argument as before, $-L$ is an upper bound for $-S$ , so by the least upper bound property,

\sup\,\p{-S} \leq -L \implies -\sup\,\p{-S} \leq L.

Thus (2) holds, so $\inf{S} = -\sup\,\p{-S}$ . $\square$

Exercise 1.

Prove that if $\inf{S}$ exists, then it is unique.

Example 5.

If $a, b$ are real numbers such that $a$ is finite and $a < b$ , then $\inf{\p{a, b}} = a$ .

Solution.

In our proof of the greatest lower bound property, we showed that $\inf{S} = -\sup\,\p{-S}$ . Applying this with $S = \p{a, b}$ , we get

\inf{\p{a, b}} = -\sup\,\p{-b, -a} = -\p{-a} = a.

Week 3 Discussion Notes

Table of Contents

Induction

Example 1.

Solution.

Example 2.

Solution.

Rational Numbers Q\QQ

Theorem (rational roots theorem)

Corollary

Proof.

Real Numbers R\RR

Definition

Definition (the real numbers)

The Least Upper Bound Property

Definition

Example 3.

Definition

Proposition

Proof.

Example 4.

Solution.

Definition

Proposition

Proof.

Exercise 1.

Example 5.

Solution.

Rational Numbers $\Q$

Real Numbers $\R$