Week 6 Discussion Notes
Table of Contents
Traces
A vertical trace of a surface is its intersection with a plane of the form or . A horizontal trace is its intersection with a plane of the form .
Example 1.
Describe the traces of .
Solution.
:
We can just substitute into the equation of the surface to get
is fixed, so this tells us that this trace is a parabola opening upwards, and simply translates the parabola:
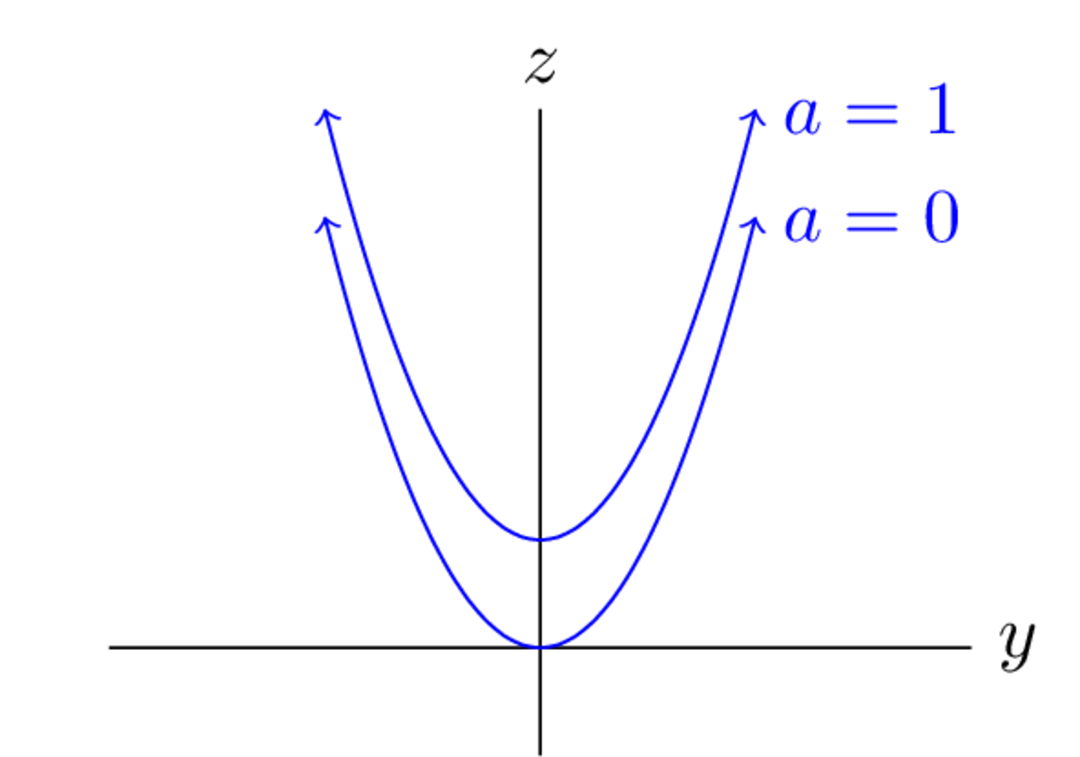
:
Similarly,
so we still get a parabola, but increasing shifts the parabola more than the above:
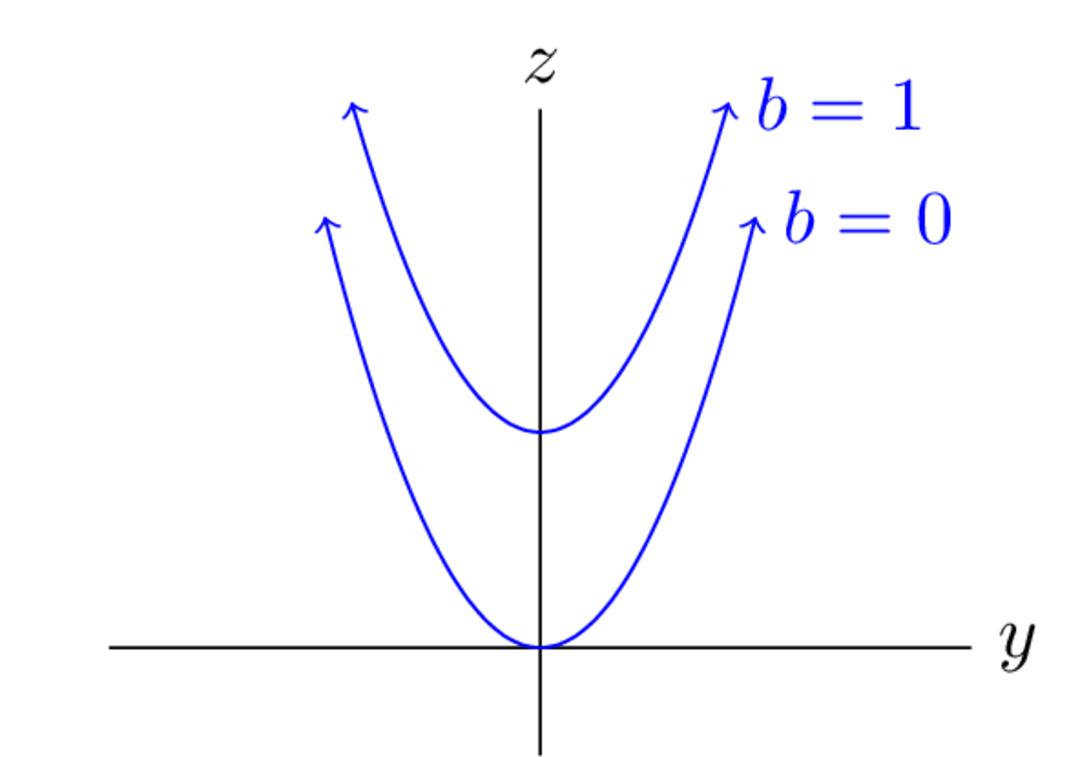
:
This one is a little different from previous ones:
Before, the traces gave us one variable as a function of the other, e.g., and . For this one, you can't solve for or without breaking things up into cases (i.e., without writing everywhere). But the equation is still something familiar to us: it's the equation of an ellipse:
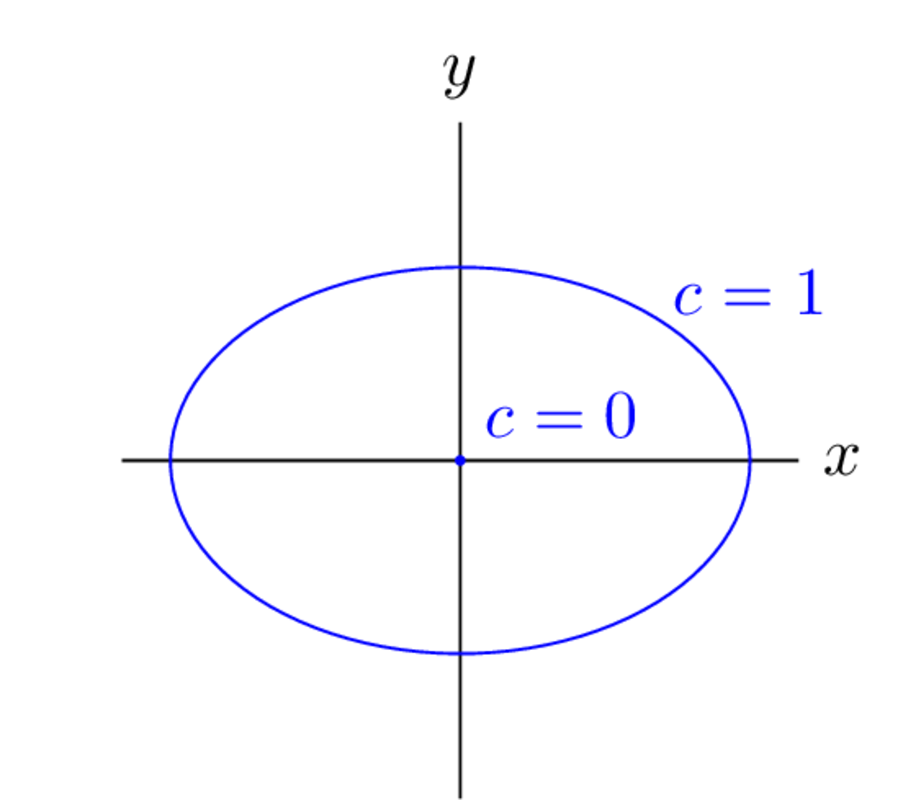
Limits
When dealing with limits, there are essentially two different problems:
- You need to show a limit does not exist.
- You can try to find different limits along different paths.
- You need to calculate a limit.
- You can try to plug in numbers using continuity.
- You can try the squeeze theorem.
Example 2.
Determine whether the following limit exists or not. If it does, calculate the limit.
Solution.
Generally, you want to try a couple paths to get a feel for the problem. If you find two different limits, then the limit doesn't exist, but if every path you try gives you the same answer, you might want to start proving that the limit exists.
I usually try the following paths first: a horizontal line, a vertical line, or a line.
Horizontal line through :
You can parametrize this by , so the limit on this path becomes
Vertical line through :
This is , so you get
line through :
The path is , so you end up with
We found two paths where the limits don't agree: gives but gives , so
Example 3.
Determine whether the following limit exists or not. If it does, calculate the limit.
Solution.
Usually, if you see sines or cosines, you can try the squeeze theorem since
for any . In our problem, we get
since is continuous at . So, by the squeeze theorem,