Week 3 Discussion Notes

Table of Contents

• Planes
• Scalar Triple Product
• Collision vs. Intersection

Planes

When specifying a line, we just need two pieces of information: a point $\vec{r}_0$ on the line and the direction $\vec{v}$ that the line points in. Then any point on the line can be represented by $\vec{r}\p{t} = \vec{r}_0 + t\vec{v}$.

Similar to a line, to specify a plane, we still need a point $\vec{r}_0$ on the plane. However, a plane doesn't really have a direction, but it does have a tilt. If you think about it, a normal vector $\vec{n}$ to the plane is a succinct way of describing tilt. Then given any point $\vec{r}$ on the line, the vector $\vec{r} - \vec{r}_0$ is parallel to the plane, so we get

Graphically,

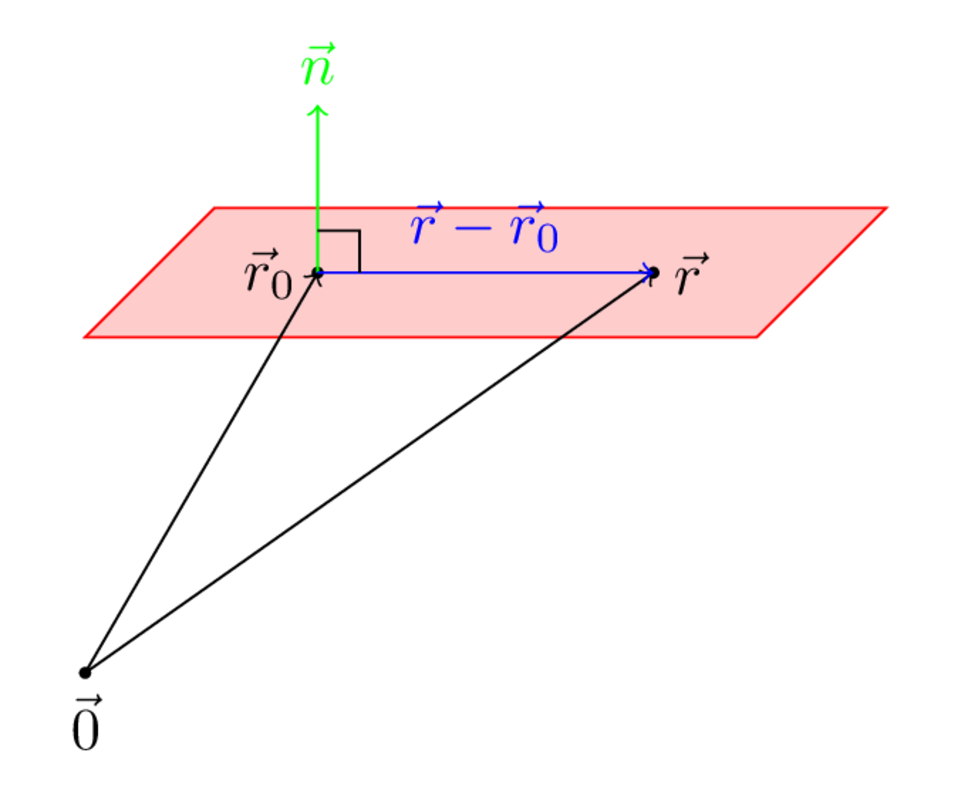
If we let $\vec{r} = \ang{x, y, z}$, $\vec{r}_0 = \ang{x_0, y_0, z_0}$, and $\vec{n} = \ang{a, b, c}$, then the equation becomes

Note that the coefficients of our normal vector $\vec{n}$ are the coefficients on $x, y, z$. This means that given the equation of a plane, you can immediately write down a normal vector just by looking at the coefficients.

Scalar Triple Product

The scalar triple product $\vec{u} \cdot \p{\vec{v} \times \vec{w}}$ is the (signed) volume of the parallelepiped spanned by $\vec{u}, \vec{v}, \vec{w}$. This means that if the scalar triple product is $0$, then the parallelepiped is flat, i.e., $\vec{u}, \vec{v}, \vec{w}$ must be coplanar.

Collision vs. Intersection

If $\vec{r}_1\p{t}$ and $\vec{r}_2\p{t}$ are two curves, then:

1. They intersect when $\vec{r}_1\p{t} = \vec{r}_2\p{s}$ (note the different variables).
2. They collide when $\vec{r}_1\p{t} = \vec{r}_2\p{t}$ (note the variables are the same).

For example:

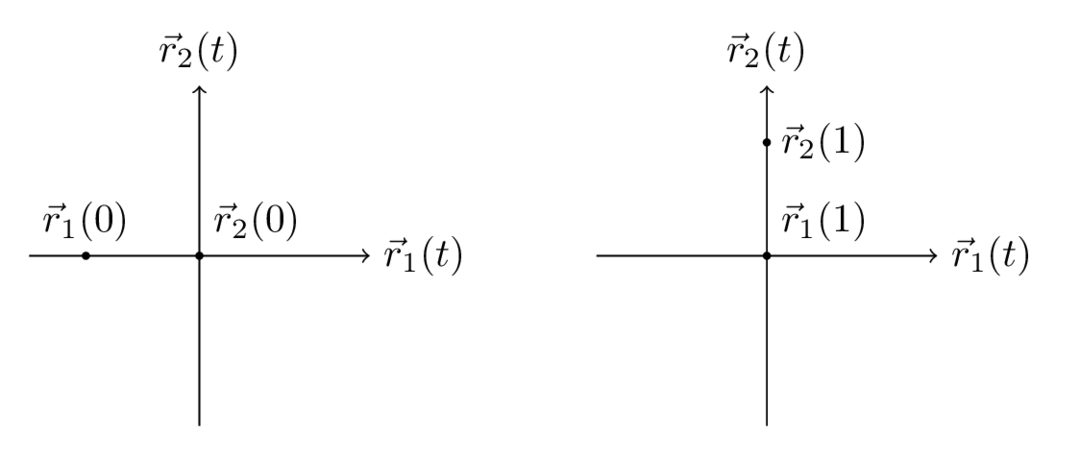
In the picture, $\vec{r}_1$ and $\vec{r}_2$ intersect because $\vec{r}_1\p{1} = \vec{r}_2\p{0}$, but they don't collide because they pass through the intersection at different times.