Week 10 Discussion Notes

Table of Contents

• Lagrange Multipliers

Lagrange Multipliers

The setup is this: we want to optimize a function $f\p{x, y}$ subject to some constraint $g\p{x, y} = c$. In other words, we want to maximize and minimize $f\p{x, y}$, where $\p{x, y}$ lives on a level curve.

With this setup, the critical points are the points that satisfy the Lagrange multiplier equation

or points where $\nabla f, \nabla g$ don't exist.

There is a technicality with this, though. If there are a global max and global min, then they have to satisfy the equation. But sometimes, you don't have a global max or a global min, so you need to have an idea of what extrema there are.

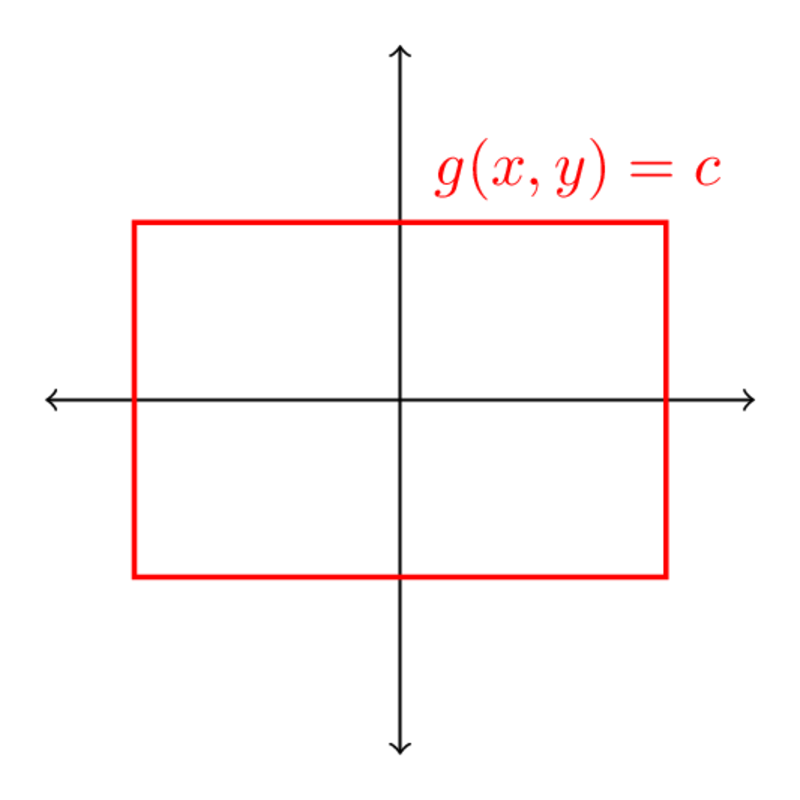
Bounded Constraints

If your constraint is bounded, then there will always be both a global min and a global max.

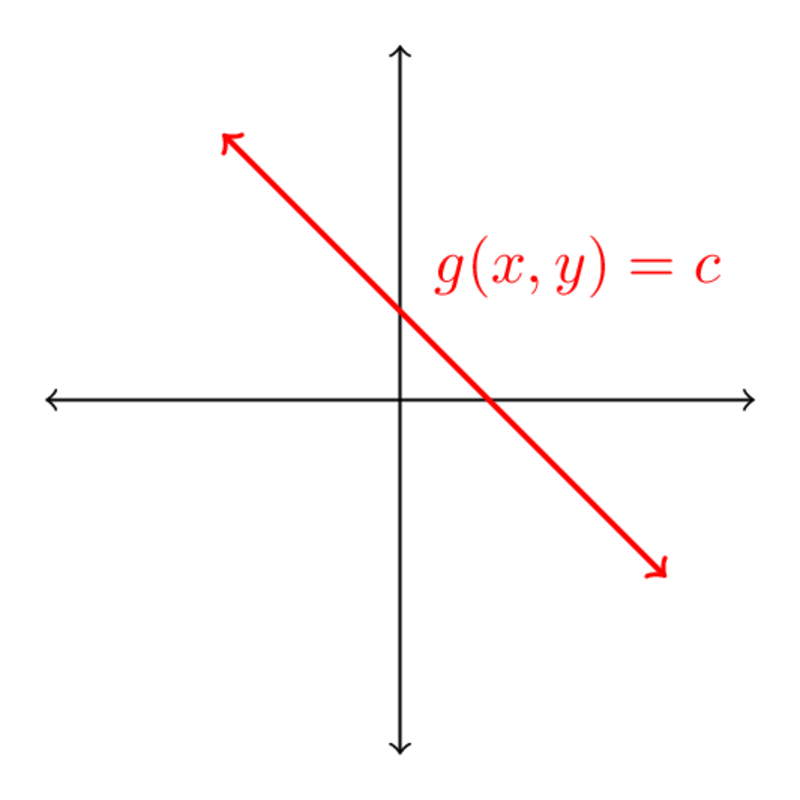
Unbounded Constraints

If your constraint is unbounded, then there's a chance that you don't have a global min or max. In this case, you'll have to figure out if you have any based on what $f$ and $g$ are.

Example 1.

Optimize $f\p{x, y} = x^2 + y^2$ subject to $2x + 3y = 6$.

Solution.

For this problem, the constraint is unbounded because it's a line. If $x$ and $y$ are large (either large positive numbers or large negative numbers), then $f\p{x, y}$ will also become very large. This tells you that $f$ doesn't have a maximum. You can prove it like this: you can solve the constraint for $x$ to get

$$x = 3 - \frac{3}{2}y.$$

Plugging this into $f\p{x, y}$, you get

$$\begin{aligned} f\p{3 - \frac{3}{2}y, y} &= \p{3 - \frac{3}{2}y}^2 + y^2. \end{aligned}$$

Then

$$\lim_{y\to\infty} f\p{3 - \frac{3}{2}y, y} = \lim_{y\to-\infty} f\p{3 - \frac{3}{2}y, y} = \infty.$$

In this situation, you still get a global minimum, so we can try the Lagrange multiplier equation. The gradients are

$$\begin{aligned} \nabla{f}\p{x, y} &= \ang{2x, 2y} \\ \nabla{g}\p{x, y} &= \ang{2, 3}, \end{aligned}$$

so the equation is

$$\ang{2x, 2y} = \lambda\ang{2, 3}.$$

The first coordinate gives us $x = \lambda$, and the second coordinate gives us $y = \frac{3\lambda}{2}$. Plugging this into the constraint,

$$2\lambda + 3\p{\frac{3\lambda}{2}} = 6 \implies \lambda = \frac{12}{13}.$$

Thus, $\p{x, y} = \p{\frac{12}{13}, \frac{18}{13}}$ is our critical point. Since there's a global minimum, it must be a critical point, and since there's only one critical point, this means that the minimum is

$$f\p{\frac{12}{13}, \frac{18}{13}} = \frac{36}{13}.$$