Week 1 Discussion Notes

Table of Contents

• Vectors

  • Basic Operations
  • Length

• Parametrizing Lines

Vectors

Basic Operations

A vector (in this class) is an ordered set of numbers. For example, $\ang{1, 2, 2}$ is a $3$-dimensional vector and $\ang{4, 7}$ is a $2$-dimensional one. There are two basic operations:

1. (vector addition) If $\vec{v} = \ang{a_1, b_1, c_1}$ and $\vec{w} = \ang{a_2, b_2, c_2}$, then $\vec{v} + \vec{w} = \ang{a_1 + a_2, b_1 + b_2, c_1 + c_2}$.
2. (scalar multiplication) If $\vec{v} = \ang{a, b, c}$ and $\lambda$ is a real number, then $\lambda\vec{v} = \ang{\lambda a, \lambda b, \lambda c}$.

In other words, you just do everything coordinate-wise. One thing to notice is that there's no standard way to multiply vectors, so things like $\vec{v} \vec{w}$ and $\frac{\vec{v}}{\vec{w}}$ are meaningless. Because of this, I strongly recommend putting the little arrows on your vectors so that mistakes are more obvious. For example, say you want to solve $\lambda \vec{v} = \vec{w}$ for $\lambda$. If you don't use the arrows, then you might end up writing something like

which doesn't really stand out. On the other hand, if you wrote

then the problem is a lot more apparent.

Length

If $\vec{v} = \ang{a, b}$, then you can draw the following picture:

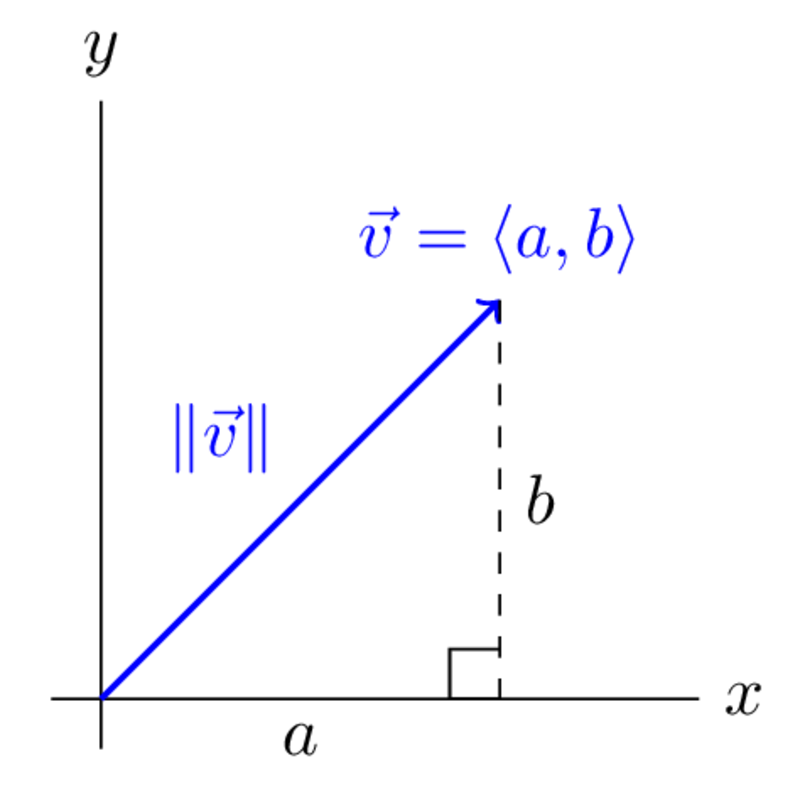
$\norm{\vec{v}}$ denotes the length of $\vec{v}$, and from the Pythagorean theorem, you get

Warning: It's not true in general that $\norm{\vec{v} + \vec{w}} = \norm{\vec{v}} + \norm{\vec{w}}$. For example, if $\vec{v} = \ang{1, 0}$ and $\vec{w} = \ang{0, 1}$, then

but

Parametrizing Lines

To specify a line, you need two pieces of information. First is a point $\vec{r}_0$ on the line:

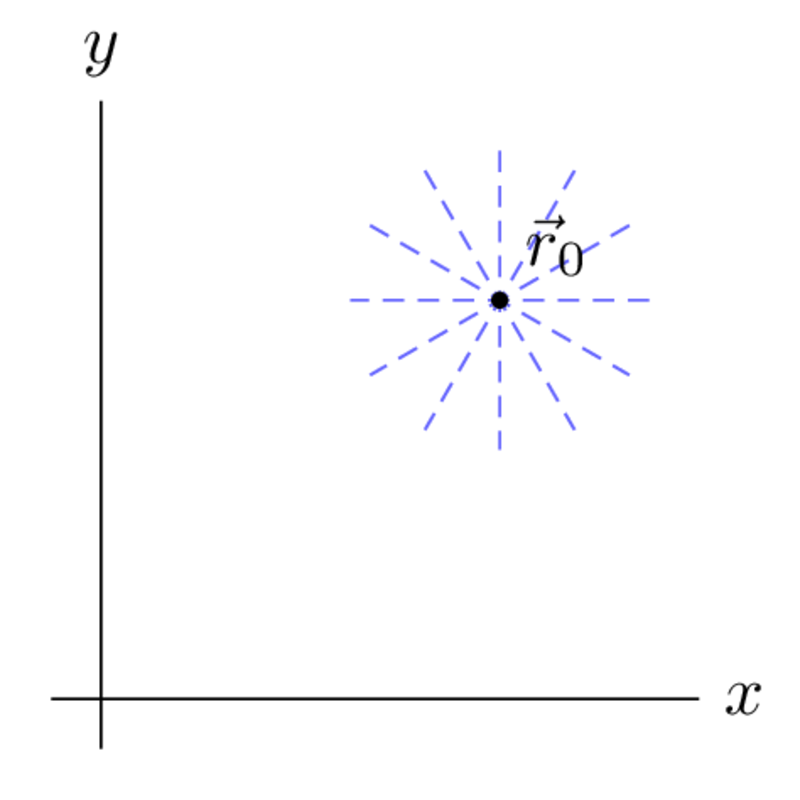
From the picture, you can see that one point is not enough. Hopefully, you can see that to uniquely specify a line, I also need to tell you the direction $\vec{v}$ that the line passes through:

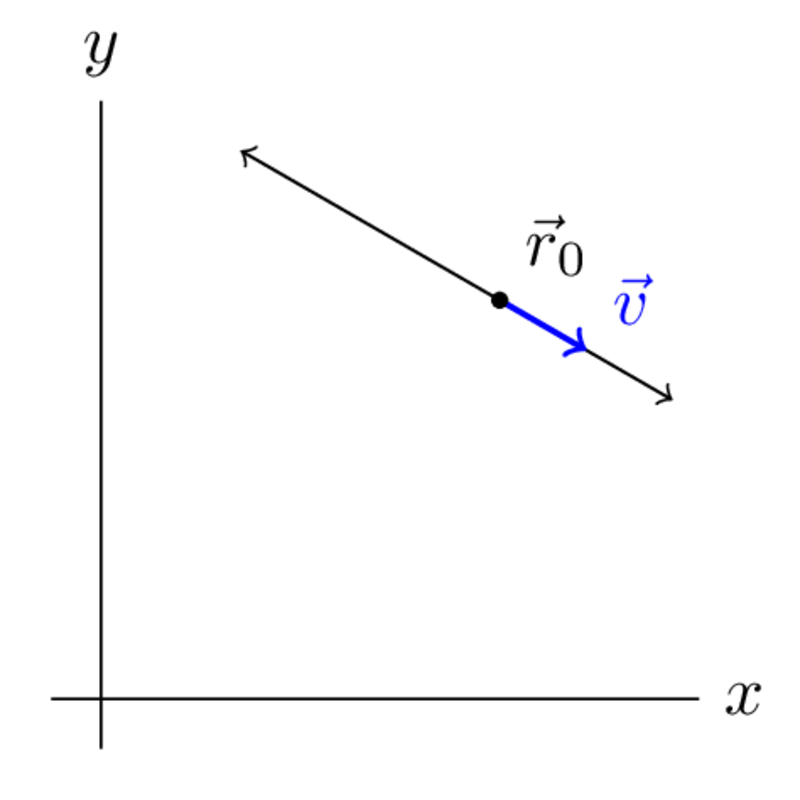
From here, you can see that if you scale $\vec{v}$, you can get any point on the line. For example:

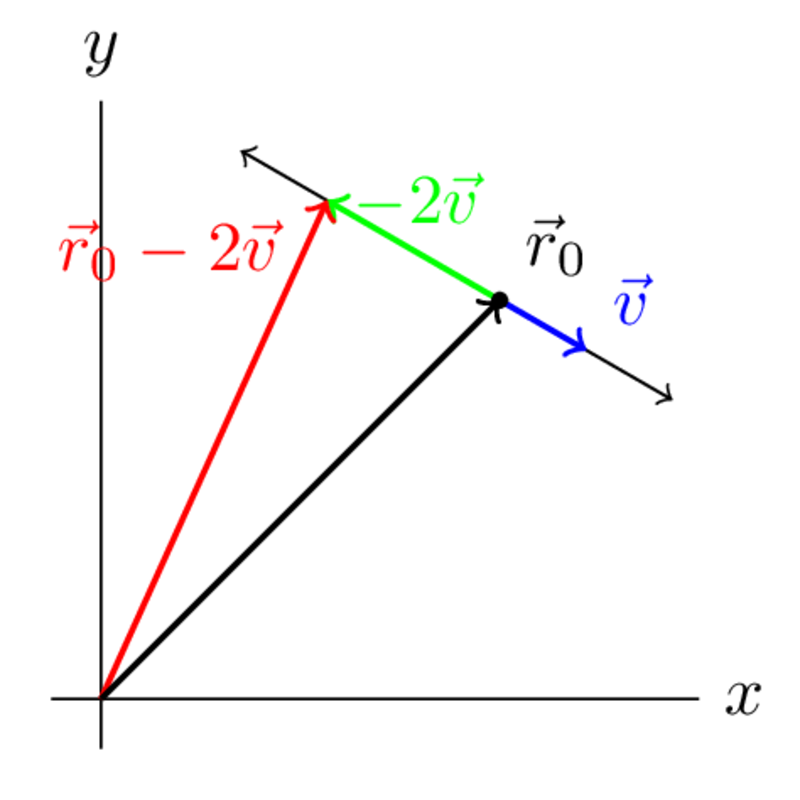
So you can parametrize the line by

Notice that you have a lot of choices for $\vec{r}_0$ and $\vec{v}$: $\vec{r}_0$ can be any point on the line, and you can replace $\vec{v}$ with any (non-zero) scalar multiple of $\vec{v}$. This means that the vector parametrization of a line is not unique.